题目内容
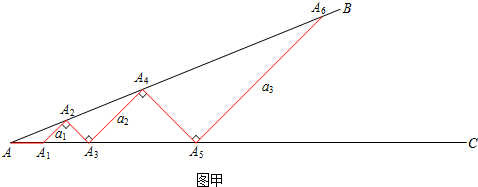
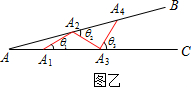
 如图,A1A2⊥A2A3,A2A3⊥A3A4,…,设AA1=A1A2=A2A3=1,若A1A2=a1,A3A4=a2,A5A6=a3,则a2=________,an=________(用含n的代数式表示)
如图,A1A2⊥A2A3,A2A3⊥A3A4,…,设AA1=A1A2=A2A3=1,若A1A2=a1,A3A4=a2,A5A6=a3,则a2=________,an=________(用含n的代数式表示)
1+ (
( +1)n-1
+1)n-1
分析:结合已知条件,根据直角三角形的性质,即可得出A1A3= ,AA3=1+
,AA3=1+ ,由A1A2∥A3A4∥A5A6,可以推出∠A=∠AA2A1=∠AA4A3=∠AA6A5,得AA3=A3A4,AA5=A5A6,即可推出a2的长度,然后推出an的关于你的表达式;
,由A1A2∥A3A4∥A5A6,可以推出∠A=∠AA2A1=∠AA4A3=∠AA6A5,得AA3=A3A4,AA5=A5A6,即可推出a2的长度,然后推出an的关于你的表达式;
解答:②∵AA1=A1A2=A2A3=1,A1A2⊥A2A3,
∴A1A3= ,AA3=1+
,AA3=1+ .
.
又∵A2A3⊥A3A4,
∴A1A2∥A3A4.
同理:A3A4∥A5A6,
∴∠A=∠AA2A1=∠AA4A3=∠AA6A5,
∴AA3=A3A4,AA5=A5A6
∴a2=A3A4=AA3=1+ ,
,
∴an=( +1)n-1.
+1)n-1.
故答案是:1+ ;(
;( +1)n-1.
+1)n-1.
点评:本题主要考查相似三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识点,解题的关键在于找到等量关系.
 (
( +1)n-1
+1)n-1分析:结合已知条件,根据直角三角形的性质,即可得出A1A3=
 ,AA3=1+
,AA3=1+ ,由A1A2∥A3A4∥A5A6,可以推出∠A=∠AA2A1=∠AA4A3=∠AA6A5,得AA3=A3A4,AA5=A5A6,即可推出a2的长度,然后推出an的关于你的表达式;
,由A1A2∥A3A4∥A5A6,可以推出∠A=∠AA2A1=∠AA4A3=∠AA6A5,得AA3=A3A4,AA5=A5A6,即可推出a2的长度,然后推出an的关于你的表达式;解答:②∵AA1=A1A2=A2A3=1,A1A2⊥A2A3,
∴A1A3=
 ,AA3=1+
,AA3=1+ .
.又∵A2A3⊥A3A4,
∴A1A2∥A3A4.
同理:A3A4∥A5A6,
∴∠A=∠AA2A1=∠AA4A3=∠AA6A5,
∴AA3=A3A4,AA5=A5A6
∴a2=A3A4=AA3=1+
 ,
,∴an=(
 +1)n-1.
+1)n-1.故答案是:1+
 ;(
;( +1)n-1.
+1)n-1.点评:本题主要考查相似三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识点,解题的关键在于找到等量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 (2013•南京二模)如图,点A1、A2、A3、A4、A5在⊙O上,且
(2013•南京二模)如图,点A1、A2、A3、A4、A5在⊙O上,且