题目内容
 如图,等边△ABC内接于⊙O,D是劣弧BC上的任一点,AD=2,则四边形ABCD的面积为( )
如图,等边△ABC内接于⊙O,D是劣弧BC上的任一点,AD=2,则四边形ABCD的面积为( )A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |
考点:全等三角形的判定与性质,等边三角形的性质,圆周角定理
专题:
分析:延长DB至M,使得MB=DC,连接AM,由全等三角形的判定定理可知△AMB≌△ADC,进而可得出S四边形ABDC=S△AMD,故可求出答案.
解答:解:如图:延长DB至M,使得MB=DC,连接AM,
△AMB≌△ADC
∴AM=AD,∠MAB=∠DAC,
又∵∠BAC=60°,
∴△MAD为正三角形,
∴S四边形ABDC=S△AMD=
.
故选:C.

△AMB≌△ADC
∴AM=AD,∠MAB=∠DAC,
又∵∠BAC=60°,
∴△MAD为正三角形,
∴S四边形ABDC=S△AMD=
| 3 |
故选:C.
点评:本题考查了全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
下列选项中不能运用平方差公式的有( )
| A、(a+b+c)(a-b+c) |
| B、(a-b+c)(-a+b-c) |
| C、(a-b+c)(a+b-c) |
| D、(-a+b+c)(-a-b-c) |
 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )A、 |
B、 |
C、 |
D、 |
下列运算正确的是( )
| A、(-2x2)3=-8x5 |
| B、x2•x3=x6 |
| C、3a2-a2=3 |
| D、(3a-4b)(3a+4b)=9a2-16b2 |
等腰三角形的两边长分别为6和12,则这个三角形的周长为( )
| A、18 | B、24 |
| C、30 | D、24或30 |
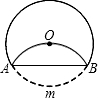 如图,⊙O的半径为6,将圆沿AB折叠后,圆弧恰好经过圆心,则弧AmB的长度为
如图,⊙O的半径为6,将圆沿AB折叠后,圆弧恰好经过圆心,则弧AmB的长度为 如图,矩形ABCD中,AB=2,AD=2
如图,矩形ABCD中,AB=2,AD=2 如图.正方形ABCD的四个顶点在⊙O上,延长BA到E,使AE=AB,连结ED.
如图.正方形ABCD的四个顶点在⊙O上,延长BA到E,使AE=AB,连结ED.