题目内容
若自然是x<y<z,a为整数,且 ,试求x,y,z.
,试求x,y,z.
解:分析由题设可知x≥1,y≥2,z≥3,所以
0≤a= +
+ +
+ =
=
又因a是整数,故a=1.若x=1,则1+ +
+ =1,
=1, +
+ =0,与题意不符,所以x≠1.
=0,与题意不符,所以x≠1.
又x≥3时,a= +
+ +
+ ≤
≤ +
+ +
+ =
=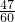 <1,也不成立,故x只能为2.
<1,也不成立,故x只能为2.
当x=2, +
+ =1-
=1- =
= .
.
令y=3,则z=6.
当x=2,y≥4时, +
+ =1-
=1- =
=
当x=2,y=4时, +
+ =
= +
+ =
= <
< ,不成立.
,不成立.
故本题只有一组解,即x=2,y=3,z=6.
答:x=2,y=3,z=6.
分析:可先设x≥1,y≥2,z≥3,根据 ,a为整数,当x=1时进行分析看是否符合;然后令x≥3时,进行分析,看看是否符合题意;最后令x=2,进行分析,看看是否符合题意,从而得到结果.
,a为整数,当x=1时进行分析看是否符合;然后令x≥3时,进行分析,看看是否符合题意;最后令x=2,进行分析,看看是否符合题意,从而得到结果.
点评:解决本题的关键是将等式转化为不等式,然后进行分类讨论.
0≤a=
 +
+ +
+ =
=
又因a是整数,故a=1.若x=1,则1+
 +
+ =1,
=1, +
+ =0,与题意不符,所以x≠1.
=0,与题意不符,所以x≠1.又x≥3时,a=
 +
+ +
+ ≤
≤ +
+ +
+ =
=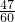 <1,也不成立,故x只能为2.
<1,也不成立,故x只能为2.当x=2,
 +
+ =1-
=1- =
= .
.令y=3,则z=6.
当x=2,y≥4时,
 +
+ =1-
=1- =
=
当x=2,y=4时,
 +
+ =
= +
+ =
= <
< ,不成立.
,不成立.故本题只有一组解,即x=2,y=3,z=6.
答:x=2,y=3,z=6.
分析:可先设x≥1,y≥2,z≥3,根据
 ,a为整数,当x=1时进行分析看是否符合;然后令x≥3时,进行分析,看看是否符合题意;最后令x=2,进行分析,看看是否符合题意,从而得到结果.
,a为整数,当x=1时进行分析看是否符合;然后令x≥3时,进行分析,看看是否符合题意;最后令x=2,进行分析,看看是否符合题意,从而得到结果.点评:解决本题的关键是将等式转化为不等式,然后进行分类讨论.

练习册系列答案
相关题目


 ,试求x,y,z.
,试求x,y,z.