题目内容
如图所示，把一张矩形纸片沿对角线折叠．（1）重合部分是什么图形？试说明理由；
（2）若CD=1，BC=
| 3 |
分析：（1）在折叠过程中，∠DBC转移到了∠EBD，但是大小并没有发生变化，又由于平行，内错角相等，所以∠DBC=∠FDB．因此构成一个等腰三角形．
（2）在三角形FED中，ED=1，EF+FB=
．
由（1）得，FD=FB，所以可根据勾股定理，列方程进行解答．
找到边长后，求出面积．
（2）在三角形FED中，ED=1，EF+FB=
| 3 |
由（1）得，FD=FB，所以可根据勾股定理，列方程进行解答．
找到边长后，求出面积．
解答：解：（1）重合部分是等腰三角形．
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠DBC=∠ADB．
又∵∠DBC=∠DBF，
∴∠DBF=∠ADB．
∴FB=FD．
（2）∵四边形ABCD是矩形，
∴∠DEB=∠C=∠A=90°，AB=ED，
又∠AFB=∠EFD，
∴△ABF≌△EDF．
∴EF=AF．
设EF=x，则x2+1=（
-x）2
解得x=
．
∴S△FED=
．
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠DBC=∠ADB．
又∵∠DBC=∠DBF，
∴∠DBF=∠ADB．
∴FB=FD．
（2）∵四边形ABCD是矩形，
∴∠DEB=∠C=∠A=90°，AB=ED，
又∠AFB=∠EFD，
∴△ABF≌△EDF．
∴EF=AF．
设EF=x，则x2+1=（
| 3 |
解得x=
| ||
| 3 |
∴S△FED=
| ||
| 6 |
点评：本题主要考查学生抽象思维能力，需要在平时生活中多加培养空间观念以及转化的能力．
练习册系列答案
相关题目
19、如图所示，把一张矩形纸片ABCD沿对角线BD折叠，将重合部分剪去，得到△ABF和△EDF．求证：△ABF≌△EDF．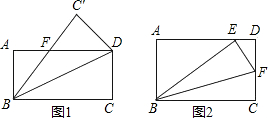
矩形折叠问题：如图所示，把一张矩形纸片沿对角线折叠，重合部分是什么图形，试说明理由．
如图所示，把一张矩形纸片ABCD沿对角线BD折叠，已知AB=6、BC=8，则BF=