题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点的横坐标分别为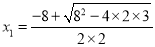 ,
, 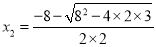 ,则此二次函数图象的对称轴为______.
,则此二次函数图象的对称轴为______.
练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点的横坐标分别为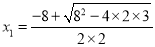 ,
, 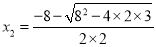 ,则此二次函数图象的对称轴为______.
,则此二次函数图象的对称轴为______.
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案