题目内容
14．
如图，△ABC是等边三角形，AD是角平分线，△ADE是等边三角形，下列结论：①AD⊥BC；②EF=FD；③BE=BD中正确个数为（ ）| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
分析 根据等腰三角形三线合一，即可一一判断．
解答 解：∵△ABC是等边三角形，△AED是等边三角形，
∴AB=AC=BC，∠BAC=60°，AE=AD=ED，∠EAD=60°，
∵∠DAB=∠DAC=30°，
∴AD⊥BC，故①正确，∠EAB=∠BAD=30°，
∴AB⊥ED，EF=DF，故②正确
∴BE=BD，故③正确，
故选A．
点评 本题考查等边三角形的性质，解题的关键是灵活应用等腰三角形的三线合一的性质解决问题，属于中考基础题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
如图，在长方形ABCD中，AB=9，BC=5，则图中四个小长方形的周长和为28．
3．某种商品的成本为每件20元，经市场调查发现，这种商品在未来40天内的日销售量m（件）与x（天）的关系如表．
未来40天内，前20天每天的价格y1（元/件）与时间x（天）的函数关系式为y1=$\frac{1}{4}$x+25（1≤x≤20且x为整数），后20天每天的价格y2（元/件）与时间x（天）的函数关系式为y2=-$\frac{1}{2}$+40（21≤x≤40且x为整数）．
（1）求日销售量m（件）与时间x（天）之间的关系式．
（2）请预测本地市场在未来40天中哪一天的日销售利润最大？最大日销售利润是多少？
（3）在实际销售的前20天中，该公司决定每销售一件商品就捐款a（a≤5）元利润给希望工程，公司看过销售记录发现，前20天中每天扣除捐款后的日销售利润随时间x（天）的增大而增大，求a的取值范围．
| 时间x（天） | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量m（件） | 94 | 90 | 84 | 76 | 24 | … |
（1）求日销售量m（件）与时间x（天）之间的关系式．
（2）请预测本地市场在未来40天中哪一天的日销售利润最大？最大日销售利润是多少？
（3）在实际销售的前20天中，该公司决定每销售一件商品就捐款a（a≤5）元利润给希望工程，公司看过销售记录发现，前20天中每天扣除捐款后的日销售利润随时间x（天）的增大而增大，求a的取值范围．
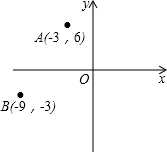如图，在平面直角坐标系中，已知点A（-3，6），B（-9，-3），以原点O为位似中心，相似比为$\frac{1}{3}$，把△ABO缩小，则点A的对应点A′的坐标是（-1，2）或（1，-2）．