题目内容
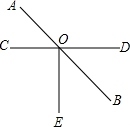 如图,两直线AB,CD相交于点O,OE⊥OC,∠BOE=
如图,两直线AB,CD相交于点O,OE⊥OC,∠BOE=| 1 | 3 |
分析:首先根据垂直可得∠COE=∠EOD=90°,设∠BOE=x°,进而得到方程x=
(90+x),解方程可得x的值,然后求出∠DOB的度数,再根据对顶角相等可得∠AOC的度数.
| 1 |
| 3 |
解答:解:∵OE⊥OC,
∴∠COE=∠EOD=90°,
设∠BOE=x°,
∵∠BOE=
∠BOC,
∴x=
(90+x),
解得:x=45,
∴∠BOE=45°,
∴∠DOB=90°-45°=45°,
∴∠AOC=45°.
∴∠COE=∠EOD=90°,
设∠BOE=x°,
∵∠BOE=
| 1 |
| 3 |
∴x=
| 1 |
| 3 |
解得:x=45,
∴∠BOE=45°,
∴∠DOB=90°-45°=45°,
∴∠AOC=45°.
点评:此题主要考查了垂直定义和对顶角的性质,关键是掌握对顶角相等.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 9、如图,两直线AB、CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=( )
9、如图,两直线AB、CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=( )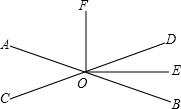 如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,
如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7, 如图,两直线AB、CD被直线EF所截,∠2=70°,下列结论正确的是( )
如图,两直线AB、CD被直线EF所截,∠2=70°,下列结论正确的是( )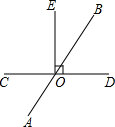 如图,两直线AB、CD相交于O点,OE⊥CD,且∠BOC=4∠BOE,试求∠AOE的度数.
如图,两直线AB、CD相交于O点,OE⊥CD,且∠BOC=4∠BOE,试求∠AOE的度数.