题目内容
(10分)如图正方形ABCD边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H。

(1)求证:BH⊥DE;
(2)当BH垂直平分DE时,求CG的长度?请说明理由。

(1)求证:BH⊥DE;
(2)当BH垂直平分DE时,求CG的长度?请说明理由。
(1)见解析;(2)

试题分析:(1)先根据正方形的性质证得△BCG≌△DCE,可得∠GBC=∠CDE,再根据Rt△DCE中∠CDE+∠CED=900,即可证得结论;
(2)由BH垂直平分DE可得BD=BE,再由BD=
 即可求得结果.
即可求得结果.(1)∵正方形ABCD
∴∠BCD=900
BC=CD
同理:CG=CE
∠GCE=900
∴∠BCD=∠GCE=900
∴△BCG≌△DCE
∴∠GBC=∠CDE
在Rt△DCE中
∠CDE+∠CED=900
∴∠GBC+∠BEH=900
∴∠BHE=1800-(∠GBC+∠BHE) =900
∴BH⊥DE
(2)当CG=
 -1时BH垂直平分DE
-1时BH垂直平分DE理由如下:若BH垂直平分DE
∴BD=BE
∵BD=

∴CG=CE=BE-BC=
 -1.
-1.点评:解答本题的关键是熟练掌握正方形的四条边相等,四个角都是直角,线段垂直平分线上的点到相等两端的距离相等。

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
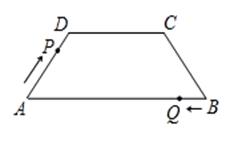
 中,AB∥DC,AD=BC=5,DC=7,AB=13,动点P从点A出发,以每秒2个单位的速度沿AD→DC→CB→BA向终点A运动,同时点Q从点B出发,以每秒1个单位的速度沿BA向终点A运动,设运动时间为t秒。(12分)
中,AB∥DC,AD=BC=5,DC=7,AB=13,动点P从点A出发,以每秒2个单位的速度沿AD→DC→CB→BA向终点A运动,同时点Q从点B出发,以每秒1个单位的速度沿BA向终点A运动,设运动时间为t秒。(12分)
 与
与 重合?
重合? . 设∠ACB=
. 设∠ACB= .(1)图中还有哪些角也等于
.(1)图中还有哪些角也等于 的值.
的值.


 中,
中,  的平分线将
的平分线将 分成
分成 和
和 两部分, 则平行四边形
两部分, 则平行四边形 ,则△CEF的周长为 .
,则△CEF的周长为 .
 ABCD中,AD=3cm,AB=2cm,则
ABCD中,AD=3cm,AB=2cm,则