��Ŀ����
ij��ҵ�����һ���Ʒ��ÿ���ijɱ���50Ԫ��Ϊ�˺������ۣ�Ͷ���г��������������г����飬���۵�����100Ԫʱ��ÿ�����������50���������۵���ÿ����1Ԫ��ÿ��Ϳɶ��۳�5������Ҫ�����۵��۲��õ��ڳɱ���
��1�����ÿ�����������y��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2��������۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3���������ҵҪʹÿ�������������4000Ԫ����ÿ����ܳɱ�������7000Ԫ����ô���۵���Ӧ������ʲô��Χ�ڣ���ÿ����ܳɱ�=ÿ���ijɱ���ÿ�����������
��1��y=��5x2+800x��27500��50��x��100������2�������۵���Ϊ80Ԫʱ��y���ֵ=4500����3�����۵���Ӧ�ÿ�����82Ԫ��90Ԫ֮�䣮 ����������������� ��1���ɡ���Ʒ����=����Ʒ�ۼۡ�-����Ʒ�ɱ��ۡ��͡�������=��������Ʒ���� ����Ʒ�����������������г�������ϵʽ�� ��2���ѣ�1�������ú�������ʽ�䷽��������������Ա�����ȡֵ��Χ���Ϳ����Ա�����ȡ...
��ϰ��ϵ�д�
 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
�����Ŀ
���꼶ѧ����ɿ���ѧϰ��������̸��ˮ���������С���Լ��ˮ���������𡱣����ڴ����꼶400��ѧ����ѡ��10��ѧ��ͳ�Ƹ��Լ�ͥһ���µĽ�ˮ������±���
��ˮ����m3�� | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
��ͥ�� | 1 | 2 | 2 | 4 | 1 |
��ô�������ݵ�������ƽ�����ֱ��ǣ�������
A. 0.4m3��0.34m3 B. 0.4m3��0.3m3 C. 0.25m3��0.34m3 D. 0.25m3��0.3m3
A ������������������ɱ����֪��0��4������ݳ��ִ�����࣬����������0��4���ų�������ѡ��ü�Ȩƽ�������㣺��0��2��1��0��25��2��0��3��2��0��4��4��0��5��1����10=3��4��10=0��34����ѡA��

 ��ͼ����D����P��һ�κ���y=mx+3��4m��m��0����ͼ����÷���������ͼ���һ�������㣻
��ͼ����D����P��һ�κ���y=mx+3��4m��m��0����ͼ����÷���������ͼ���һ�������㣻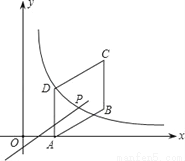
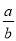 C. a��b D. a��b
C. a��b D. a��b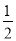 )��1��
)��1��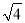 ��____��
��____��
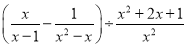 �����ө�1��0��1��2��ѡ��һ�����ʵ��������ʽ��ֵ��
�����ө�1��0��1��2��ѡ��һ�����ʵ��������ʽ��ֵ��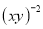 ��
��