Question

【题目】如图，在平面直角坐标系中，矩形OABC的边OA，OC分别在x轴、y轴上，点B坐标为（4，t）（t＞0），二次函数y=x2+bx（b＜0）的图象经过点B，顶点为点D．

（1）当t=12时，顶点D到x轴的距离等于；
（2）点E是二次函数y=x2+bx（b＜0）的图象与x轴的一个公共点（点E与点O不重合），求OEEA的最大值及取得最大值时的二次函数表达式；
（3）矩形OABC的对角线OB、AC交于点F，直线l平行于x轴，交二次函数y=x2+bx（b＜0）的图象于点M、N，连接DM、DN，当△DMN≌△FOC时，求t的值．

Answer 1

【答案】
（1）
（2）解：将y=0代入抛物线的解析式得：x2+bx=0，解得x=0或x=﹣b，

∵OA=4，

∴AE=4﹣（﹣b）=4+b．

∴OEAE=﹣b（4+b）=﹣b2﹣4b=﹣（b+2）2+4，

∴OEAE的最大值为4，此时b的值为﹣2，

∴抛物线的表达式为y=x2﹣2x．

（3）解：过D作DG⊥MN，垂足为G，过点F作FH⊥CO，垂足为H．

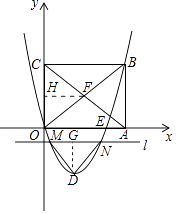
∵△DMN≌△FOC，

∴MN=CO=t，DG=FH=2．

∵D（﹣ ，﹣ ），

∴N（﹣ + ，﹣ +2），即（ ， ）．

把点N和坐标代入抛物线的解析式得： =（ ）2+b（ ），

解得：t=±2 ．

∵t＞0，

∴t=2 ．

【解析】（1）当t=12时，B（4，12）．

将点B的坐标代入抛物线的解析式得：16+4b=12，解得：b=﹣1，

∴抛物线的解析式y=x2﹣x．

∴y=（x﹣ ）2﹣ ．

∴D（ ， ）．

∴顶点D与x轴的距离为 ．

所以答案是： ．