题目内容
12.在△ABC中,已知AD是角平分线,AE是高,若∠B=42°,∠C=66°,求∠DAE的度数.分析 根据三角形的内角和定理求出∠BAC的度数,再根据AD是△BAC的角平分线,求出∠DAC的度数,减去∠EAC的度数即为∠DAE的度数.
解答 解:如图,
∵∠B=42°,∠C=66°,
∴∠BAC=∠180°-42°-66°=72°,
∵AD是△BAC的角平分线,
∴∠DAC=72°×$\frac{1}{2}$=36°,
∵∠AED=90°,∠C=66°,
∴∠EAC=90°-66°=24°,
∴∠DAE=36°-24°=12°.
点评 本题考查了三角形的内角和定理,熟悉直角三角形两锐角互余和三角形的内角和等于180°是解题的关键.

练习册系列答案
相关题目
2.下列各数中,最大的数是( )
| A. | 1 | B. | 0 | C. | -2 | D. | -1 |
5.如果|x+y-3|=2x+2y,则(x+y)3等于( )
| A. | 1 | B. | -27 | C. | 1或-27 | D. | 无法确定 |
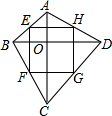 如图,若AC=BD,AC⊥BD,E,F,G,H分别是AB,BC,CD的中点.求证:四边形EFGH为正方形.
如图,若AC=BD,AC⊥BD,E,F,G,H分别是AB,BC,CD的中点.求证:四边形EFGH为正方形.