题目内容
一个三角形的边长分别为a，a，b，另一个三角形的边长分别为b，b，a，其中a＞b，若两个三角形的最小内角相等，
的值等于
- A.
- B.
- C.
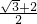
- D.
B
分析：根据余弦定理，求出最小角的余弦值，建立相等关系，解方程即可．
解答：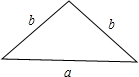
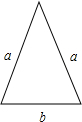解：余弦定理：a，a，b中最小内角为边b所对，cosx=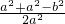
b，b，a中最小内角为边b所对，cosy=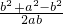
∵x=y，
∴=
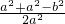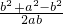
解方程得：=．
故选B．
点评：本题的关键是根据余弦定理，利用两三角形中有一个等角，建立等式，解方程求值．
分析：根据余弦定理，求出最小角的余弦值，建立相等关系，解方程即可．
解答：
解：余弦定理：a，a，b中最小内角为边b所对，cosx=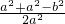b，b，a中最小内角为边b所对，cosy=
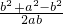
∵x=y，
∴
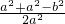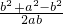
=解方程得：
=．故选B．
点评：本题的关键是根据余弦定理，利用两三角形中有一个等角，建立等式，解方程求值．
练习册系列答案
相关题目
一个三角形的边长分别为a，a，b，另一个三角形的边长分别为b，b，a，其中a＞b，若两个三角形的最小内角相等，
的值等于（ ）
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
的值等于（ ）
