题目内容
【题目】如图，反比例函数
的图象与正比例函数
图象交于点
，且点的横坐标为2.
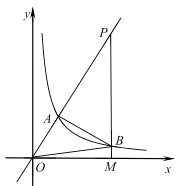
（1）求反比例函数的表达式；
（2）若射线
上有一点
，且
，过点作
与
轴垂直，垂足为
，交反比例函数图象于点
，连接
，
，请求出
的面积.
（3）定义：横纵坐标均为整数的点称为“整点”.在（2）的条件下，请探究边
，
与反比例函数图象围成的区域内（不包括边界）“整点”的个数.
【答案】（1）
（2）8（3）12
【解析】
（1）把
代入
得
,求出点A的坐标，代入反比例函数即可求出反比例函数的表达式；
（2）根据
，得到
，即可求出点
，把
代入得
，即可求出点
，过点
作
轴，交
于点
,把代入得
，求出点
进而求出
根据
即可求解.
（3）
，可求所求区域内，
，
可取整数值为3，4，5，把
分别代入和，得
，
，所以所求区域内， 
，y可取整数值为3，4；同理求出
，
即可.
（1）把代入得，∴
把代入
得
，所以
（2）如图，∵
∴ ∴
把代入得，∴
过点作轴，交于点
把
代入得，
∴
∴
∴
（3） ∴所求区域内， ，可取整数值为3，4，5
把分别代入和，得，
所以所求区域内， ，y可取整数值为3，4；
同理可知时，
，
可取整数值为2，3，4，5；
时，
，可取整数值为2，3，4，5，6，7；
综上所述，整点个数总共12个.
天天练口算系列答案
【题目】某度假村拥有客房40间，该度假村在经营中发现每间客房日租金x(元)与每日租出的客房数(y)有如下关系：
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识求出每日租出的客房数y(间)与每间客房的日租金x(元)之间的关系式．
(2)已知租出的每间客房每日需要清洁费80元，未租出的每间客房每日需要清洁费40元．含x(x≥200)的代数式填表：
租出的客房数 | ______ | 未租出的客房数 | ______ |
租出的每间客房的日收益 | ______ | 所有未租出的客房每日的清洁费 | ______ |
(3)若你是该度假村的老板，你会将每间客房的日租金定为多少元，才能使度假村获得最大日收益？最大日收益是多少元？
