题目内容
 (2012•洛阳二模)如图,已知反比例函数y=
(2012•洛阳二模)如图,已知反比例函数y=| k |
| x |
| 1 |
| 2 |
(1)求这两个函数的解析式;
(2)根据所给条件,请直接写出当x>0时不等式-x+b<
| k |
| x |
0<x<1或x>4
0<x<1或x>4
;(3)设该直线与x轴、y轴分别交于A,B两点,与反比例函数图象的另一个交点为P,连结OP、OQ,求△OPQ的面积.
分析:(1)根据图象上的点来求出函数解析式;
(2)根据图象可直接写出解集;
(3)分别求出A、B、P坐标,然后根据S△OPQ=S△ABO-S△POB-S△QOA即可求出面积.
(2)根据图象可直接写出解集;
(3)分别求出A、B、P坐标,然后根据S△OPQ=S△ABO-S△POB-S△QOA即可求出面积.
解答:解:(1)反比例函数y=
(k≠0)的图象经过点(
,8),
把点代入可得:k=xy=
×8=4,
故反比例函数解析式为:y=
,
∵点Q是直线y=-x+b与该反比例函数的交点,
∴m=
=1,
则点Q的坐标为(4,1),
把点Q代入直线解析式得:1=-4+b,
解得:b=5,
故直线的解析式为:y=-x+5;
(2)由图可知,解集为:0<x<1或x>4;
(3)根据直线解析式:y=-x+5,
可得直线与x轴y轴的交点分别为:A(5,0),B(0,5),
联立直线与反比例函数解析式,
,
解得:
或
,
即P点坐标为(1,4),
过P作PE垂直y轴于E,过Q作QF垂直x轴于F,
则S△OPQ=S△ABO-S△POB-S△QOA=
×OA•OB-
×OB•PE-
×OA×QF=
×5×5-
×5×1-
×5×1=
.
| k |
| x |
| 1 |
| 2 |
把点代入可得:k=xy=
| 1 |
| 2 |
故反比例函数解析式为:y=
| 4 |
| x |
∵点Q是直线y=-x+b与该反比例函数的交点,
∴m=
| 4 |
| 4 |
则点Q的坐标为(4,1),
把点Q代入直线解析式得:1=-4+b,
解得:b=5,
故直线的解析式为:y=-x+5;
(2)由图可知,解集为:0<x<1或x>4;
(3)根据直线解析式:y=-x+5,

可得直线与x轴y轴的交点分别为:A(5,0),B(0,5),
联立直线与反比例函数解析式,
|
解得:
|
|
即P点坐标为(1,4),
过P作PE垂直y轴于E,过Q作QF垂直x轴于F,
则S△OPQ=S△ABO-S△POB-S△QOA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题,难度适中,解答本题的关键是根据点的坐标求解析式和根据解析式求点的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
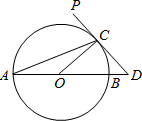 (2012•洛阳二模)如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=
(2012•洛阳二模)如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=
