题目内容
（2012•洛阳二模）如图，在矩形纸片ABCD中，AB=3，AD=1，点P在线段AB上运动，设AP=x，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．那么四边形EPFD为菱形的x的取值范围是
1≤x≤3
1≤x≤3
．分析：由要使四边形EPFD为菱形，则需DE=EP=FP=DF，可得当点P与点A重合时，AP最小；当点P与点B重合时，AP最大，继而求得四边形EPFD为菱形的x的取值范围．
解答：
解：∵要使四边形EPFD为菱形，则需DE=EP=FP=DF，
∴如图1：当点P与点A重合时，AP=AD=1，此时AP最小；
如图2：当点P与B重合时，AP=AB=3，此时AP最大；
∴四边形EPFD为菱形的x的取值范围是：1≤x≤3．
故答案为：1≤x≤3．
解：∵要使四边形EPFD为菱形，则需DE=EP=FP=DF，∴如图1：当点P与点A重合时，AP=AD=1，此时AP最小；
如图2：当点P与B重合时，AP=AB=3，此时AP最大；
∴四边形EPFD为菱形的x的取值范围是：1≤x≤3．
故答案为：1≤x≤3．
点评：此题考查了菱形的判定与性质、折叠的性质以及矩形的性质．此题难度适中，注意掌握分类讨论思想与数形结合思想的应用．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
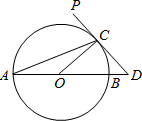（2012•洛阳二模）如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且CO=CD，则∠PCA=