题目内容
如图1,图2…、图m是边长均大于2的三角形、四边形、…、凸n边形.分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、n条弧.

(1)图1中3条弧的弧长的和为______,图2中4条弧的弧长的和为______;
(2)求图m中n条弧的弧长的和(用n表示).
解:(1)利用弧长公式可得
 +
+ +
+ =π,
=π,
因为n1+n2+n3=180°.
同理,四边形的= +
+ +
+ +
+ =2π,
=2π,
因为四边形的内角和为360度;
(2)n条弧= +
+ +
+ +
+ +…=
+…= =(n-2)π.
=(n-2)π.
分析:(1)利用弧长公式和三角形和四边形的内角和公式代入计算;
(2)利用多边形的内角和公式和弧长公式计算.
点评:本题综合考查了多边形的内角和和弧长公式的应用.
 +
+ +
+ =π,
=π,因为n1+n2+n3=180°.
同理,四边形的=
 +
+ +
+ +
+ =2π,
=2π,因为四边形的内角和为360度;
(2)n条弧=
 +
+ +
+ +
+ +…=
+…= =(n-2)π.
=(n-2)π.分析:(1)利用弧长公式和三角形和四边形的内角和公式代入计算;
(2)利用多边形的内角和公式和弧长公式计算.
点评:本题综合考查了多边形的内角和和弧长公式的应用.

练习册系列答案
相关题目
正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上,分别连接BD、BF、FD,得到 BFD.
BFD.
(1)在图1、图2、图3中,若正方形CEFG的边长分别为1、3、4,且正方形ABCD的边长均为3,请通过计算填写下表:
图1 图2 图3
| 正方形CEFG的边长 | 1 | 3 | 4 |
 BFD的面积 BFD的面积 | | | |
 ,正方形ABCD的边长为
,正方形ABCD的边长为 ,猜想
,猜想 的大小,并结合图3证明你的猜想.
的大小,并结合图3证明你的猜想.  运动的路程s与运动时间t(秒)之间的函数图象,图3是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分.
运动的路程s与运动时间t(秒)之间的函数图象,图3是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分.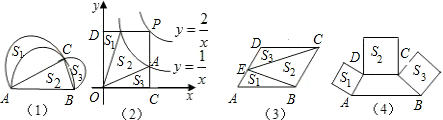
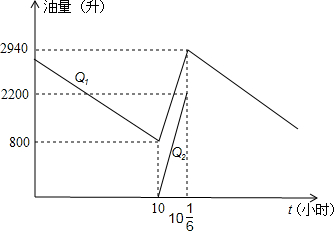 (1)求运输飞机起飞时油箱的油量;
(1)求运输飞机起飞时油箱的油量; 类似地,图2所示的算筹图我们可以表述为( )
类似地,图2所示的算筹图我们可以表述为( )
 B.
B. C.
C. D.
D.