Question

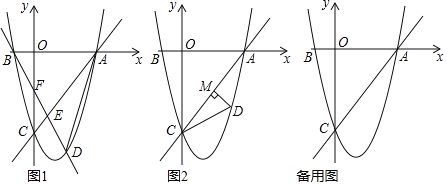
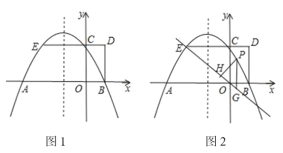
【题目】如图1，抛物线y＝ax2+bx+2与x轴交于A，B两点，与y轴交于点C，AB＝4，矩形OBDC的边CD＝1，延长DC交抛物线于点E．

（1）求抛物线的解析式；

（2）如图2，点P是直线EO上方抛物线上的一个动点，过点P作y轴的平行线交直线EO于点G，作PH⊥EO，垂足为H．设PH的长为l，点P的横坐标为m，求l与m的函数关系式（不必写出m的取值范围），并求出l的最大值．

Answer 1

【答案】（1）y＝x2x+2；（2）l=+，最大值为.

【解析】

（1）由条件可求得A、B的坐标，利用待定系数法可求得抛物线解析式；

（2）可先求得E点坐标，从而可求得直线OE解析式，可知，用m可表示出PG的长，从而可表示出l的长，再利用二次函数的性质可求得其最大值．

（1）∵矩形OBDC的边CD＝1，

∴OB＝1，

由AB＝4，得OA＝3，

∴A（﹣3，0），B（1，0），

∵抛物线y＝ax2+bx+2与x轴交于A，B两点，

∴a+b+2=0，9a－3b+2=0，

解得：a=，b=，

∴抛物线解析式为y＝x2x+2；

（2）在y＝x2x+2中，

当y＝2时，x＝0或x＝﹣2，

∴E（﹣2，2），

∴直线OE解析式为y＝﹣x，∠PGH＝∠COE＝45°，

∵P（m，m2m+2），PG∥y轴，

∴G（m，﹣m），

∴PG＝m2m+2﹣（﹣m）

＝+，

∵∠PGH＝∠COE＝45°，

∴l＝PG

＝+，

∴当m＝时，l有最大值，最大值为.