题目内容
如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
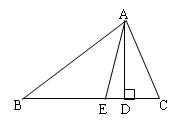
(1)若∠C-∠B=30°,则∠DAE=________.
(2)若∠C-∠B=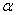 (∠C>∠B),求∠DAE的度数(用含
(∠C>∠B),求∠DAE的度数(用含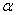 的代数式表示).
的代数式表示).


(1)若∠C-∠B=30°,则∠DAE=________.
(2)若∠C-∠B=
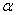 (∠C>∠B),求∠DAE的度数(用含
(∠C>∠B),求∠DAE的度数(用含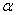 的代数式表示).
的代数式表示).(1) 15°
(2)∠DAE=1/2∠BAC-∠CAD=1/2(180°-∠B-∠C)-(90°-∠C)=1/2(∠C-∠B)=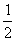
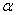
(2)∠DAE=1/2∠BAC-∠CAD=1/2(180°-∠B-∠C)-(90°-∠C)=1/2(∠C-∠B)=
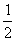
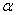
试题分析:根据三角形的内角和定理、角平分线定义可以求得∠DAE=
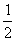 (∠C-∠B)。
(∠C-∠B)。(1)∵AD⊥BC于D,AE平分∠BAC,
∴∠DAE=90°-∠AED
=90°-(∠B+∠BAE)
=90°-(∠B+
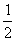 ∠BAC)
∠BAC)=90°-(∠B+90°-
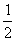 ∠B-
∠B-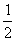 ∠C)
∠C)=
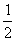 (∠C-∠B)
(∠C-∠B)=15°;
(2)∠DAE=1/2∠BAC-∠CAD=1/2(180°-∠B-∠C)-(90°-∠C)=
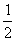 (∠C-∠B)=
(∠C-∠B)=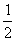
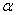
点评:此题综合运用了三角形的内角和定理、三角形的外角的性质以及角平分线定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
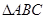 中至多有一个直角或钝角”的反设是 .
中至多有一个直角或钝角”的反设是 .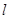 . 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号. 他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东
. 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号. 他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东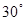 方向,甲、乙的游泳速度均是2米/秒.问谁先到达B处?请说明理由.
方向,甲、乙的游泳速度均是2米/秒.问谁先到达B处?请说明理由.
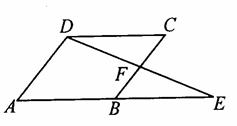


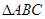 中,
中, 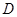 是
是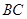 边上的一点,
边上的一点, 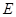 是
是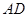 的中点, 过
的中点, 过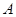 点作
点作 的延长线于点
的延长线于点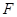 , 且
, 且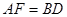 , 连接
, 连接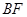 .
.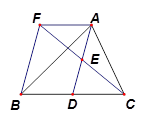
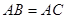 , 试判断四边形
, 试判断四边形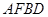 的形状, 并证明你的结论.
的形状, 并证明你的结论.