ĢāÄæÄŚČŻ
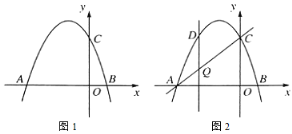
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½![]() ÓėxÖį½»ÓŚA£¬C£ØAŌŚCµÄ×ó²ą£©£¬µćBŌŚÅ×ĪļĻßÉĻ£¬Ęäŗį×ų±źĪŖ1£¬Į¬½ÓBC£¬BO£¬µćFĪŖOBÖŠµć£®
ÓėxÖį½»ÓŚA£¬C£ØAŌŚCµÄ×ó²ą£©£¬µćBŌŚÅ×ĪļĻßÉĻ£¬Ęäŗį×ų±źĪŖ1£¬Į¬½ÓBC£¬BO£¬µćFĪŖOBÖŠµć£®

£Ø1£©ĒóÖ±ĻßBCµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČōµćDĪŖÅ×ĪļĻßµŚĖÄĻóĻŽÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓBD£¬CD£¬µćEĪŖxÖįÉĻŅ»¶Æµć£¬µ±”÷BCDµÄĆ껿µÄ×ī“óŹ±£¬ĒóµćDµÄ×ų±ź£¬¼°|FE©DE|µÄ×ī“óÖµ£»
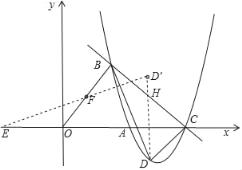
£Ø3£©ČēĶ¼2£¬ČōµćGÓėµćB¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖį¶Ō³Ę£¬Ö±ĻßBGÓėyÖį½»ÓŚµćM£¬µćNŹĒĻ߶ĪBGÉĻµÄŅ»¶Æµć£¬Į¬½ÓNF£¬MF£¬µ±”ĻNFO£½3”ĻBNFŹ±£¬Į¬½ÓCN£¬½«Ö±ĻßBOČʵćOŠż×Ŗ£¬¼ĒŠż×ŖÖŠµÄÖ±ĻßBOĪŖB”äO£¬Ö±ĻßB”äOÓėÖ±ĻßCN½»ÓŚµćQ£¬µ±”÷OCQĪŖµČŃüČż½ĒŠĪŹ±£¬ĒóµćQµÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©y£½©![]() x+
x+![]() £»£Ø2£©D£Ø
£»£Ø2£©D£Ø![]() £¬©
£¬©![]() £©£»|FE©DE|µÄ×ī“óÖµĪŖ
£©£»|FE©DE|µÄ×ī“óÖµĪŖ![]() £»£Ø3£©µćQµÄ×ų±źĪŖQ1£Ø
£»£Ø3£©µćQµÄ×ų±źĪŖQ1£Ø![]() £¬
£¬![]() £©£¬Q2£Ø
£©£¬Q2£Ø![]() £¬
£¬![]() £©£¬Q3£Ø
£©£¬Q3£Ø![]() ©
©![]() £¬
£¬![]() £©£¬Q4£Ø
£©£¬Q4£Ø![]() +
+![]() £¬©
£¬©![]() £©£®
£©£®
”¾½āĪö”æ
£Ø1£©ĮīÅ×ĪļĻßy£½0£¬Ēó³öµćCµÄ×ų±ź£¬ŌŁĮīx£½1£¬Ēó³öµćB×ų±ź£¬“ż¶ØĻµŹż·ØĒó³öÖ±ĻßBCµÄ½āĪöŹ½£»
£Ø2£©Čż½ĒŠĪĆ껿×īÖµ×Ŗ»»³ÉĒóDHµÄ×ī“óÖµ£¬Č»ŗóĄūÓƶž“ĪŗÆŹżµÄĒó×īÖµĪŹĢā½ā¾öµćDµÄ×ų±ź£¬|FEDE|µÄ×ī“óÖµ£¬æɽ«µćDŗĶµćF×Ŗ»»µ½xÖįµÄĶ¬Ņ»²ą£¬ŌŁĄūÓĆ¹²Ļߏ±²īÖµ×ī“óĒó³öĻ߶Ī³¤¶Č¼“æÉ£®
£Ø3£©ÕŅµČŃüČż½ĒŠĪĪŹĢā£¬ŅŖ·ÖĄąĢÖĀŪ£¬ŅŌOCĪŖŃü£¬»ņŅŌOCĪŖµ×¶¼æÉŅŌ£¬ĄūÓĆ”ĻOCNµÄÕżĒŠÖµĒó³ö±ßÖ®¼äµÄ±ČĄż¹ŲĻµ£¬Ēó³öµćQµÄ×ų±ź£®
£Ø1£©Įīy£½0£¬½āµĆx1£½![]() £¬x2£½
£¬x2£½![]() £¬
£¬
”ąA£Ø![]() £¬0£©£¬B£Ø
£¬0£©£¬B£Ø![]() £¬0£©
£¬0£©
µ±x£½1Ź±£¬y£½2![]()
”ąB£Ø1£¬2![]() £©
£©
ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖy£½kxb“śČėµćBŗĶC
 £¬
£¬
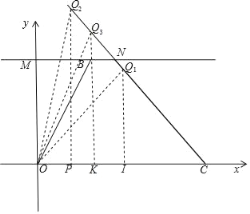
½āµĆ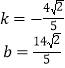
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy£½![]() ;
;
£Ø2£©ÉčµćD£Øm£¬![]() £©
£©
¹żµćD×÷xÖįµÄĘ½ŠŠĻߣ¬½»BCÓŚµćH£¬
ŌņµćH£Øm£¬©![]() m+
m+![]() £©
£©
HD£½©![]() m+
m+![]() ©£Ø
©£Ø![]() £©£½©
£©£½©![]() £Øm©
£Øm©![]() £©2+
£©2+![]()
”ąµ±m£½![]() Ź±£¬HDČ”×ī“óÖµ£¬“ĖŹ±S”÷BCDµÄĆ껿Ȕ×ī“óÖµ£®
Ź±£¬HDČ”×ī“óÖµ£¬“ĖŹ±S”÷BCDµÄĆ껿Ȕ×ī“óÖµ£®
D£Ø![]() £¬
£¬![]() £©
£©
×÷D¹ŲÓŚxÖįµÄ¶Ō³ĘµćD”ä
ŌņD”ä£Ø![]() £¬
£¬![]() £©
£©
Į¬½ÓD”äH½»xÖįÓŚŅ»µćE£¬“ĖŹ±D”äE©FE×ī“󣬼“ĪŖD”äFµÄ³¤¶Č
”ßFĪŖOBµÄÖŠµć
”ąF£Ø![]() £¬
£¬![]() £©
£©
”ąD”äF£½![]()
”ą|FE©DE|µÄ×ī“óÖµĪŖ![]() £®
£®
£Ø3£©ÓÉĢāŅāæÉÖŖM£Ø0£¬2![]() £©
£©
”ß”ĻNFO£½3”ĻBNF
”ą”ĻFBN£½2”ĻBNF
×÷”ĻFBNµÄ½ĒĘ½·ÖĻß½»xÖįÓŚµćE
Ōņ”ĻOBE£½”ĻEBG£½”ĻOEB£½”ĻBNF
¹żµćB×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖµćJ

ŌņJ£Ø1£¬0£©
”ßOB£½![]() £½3
£½3
”ąOE£½3
”ąEJ£½2
”ßBJ£½2![]()
”ątan”ĻBEJ£½![]() £¬
£¬
”ątan”ĻBNF£½![]() £¬
£¬
¹żµćF×÷MNµÄ“¹Ļߣ¬“¹×ćĪŖD
ŌņFD£½![]() £¬
£¬
”ąND£½1
”ąN£Ø![]() £¬2
£¬2![]() £©
£©
Į¬½ÓNC
”ßtan”ĻNCO£½![]()
¢Łµ±OQ1µČÓŚCQ1Ź±£¬¹żµćQ1×÷OCµÄ“¹Ļߣ¬“¹×ćĪŖI
”ßOC£½![]()
”ąCI£½![]()
”ąQ1I£½![]()
”ąQ1£Ø![]() £¬
£¬![]() £©
£©
¢Śµ±OC£½CQ3Ź±£¬¹żµćQ3×÷OCµÄ“¹Ļߣ¬“¹×ćĪŖK
”ßOC£½![]() £¬”ąCQ3£½
£¬”ąCQ3£½![]() £¬
£¬
CK£½![]() £¬Q3K£½
£¬Q3K£½![]()
”ąQ3£Ø![]() £¬
£¬![]() £©
£©
¢Ūµ±OQ2£½OCŹ±£¬¹żµćQ2×÷OCµÄ“¹Ļߣ¬“¹×ćĪŖP
”ßOC£½3£¬”ąOQ2£½3
ÉčPC£½a£¬ŌņQ2P£½![]() a£¬OP£½
a£¬OP£½![]() ©
©![]() a
a
øł¾Ż¹“¹É¶ØĄķ½āµĆa£½![]()
”ąQ2£Ø![]() £¬
£¬![]() £©
£©
¢Üµ±Q4ŌŚNCµÄŃÓ³¤ĻßÉĻŹ±£¬CQ4£½OC
Ķ¬ĄķæÉµĆ£¬Q4£Ø![]() £¬
£¬![]() £©
£©
×ŪÉĻĖłŹö£ŗµćQµÄ×ų±źĪŖQ1£Ø![]() £¬
£¬![]() £©£¬Q2£Ø
£©£¬Q2£Ø![]() £¬
£¬![]() £©£¬Q3£Ø
£©£¬Q3£Ø![]() £¬
£¬![]() £©£¬Q4£Ø
£©£¬Q4£Ø![]() £¬
£¬![]() £¬£©£®
£¬£©£®

 ĢŅĄīĪÄ»ÆæģĄÖŹī¼ŁĪäŗŗ³ö°ęÉēĻµĮŠ“š°ø
ĢŅĄīĪÄ»ÆæģĄÖŹī¼ŁĪäŗŗ³ö°ęÉēĻµĮŠ“š°ø ÓÅŠćÉśæģĄÖ¼ŁĘŚĆæŅ»ĢģČ«ŠĀŗ®¼Ł×÷Ņµ±¾ĻµĮŠ“š°ø
ÓÅŠćÉśæģĄÖ¼ŁĘŚĆæŅ»ĢģČ«ŠĀŗ®¼Ł×÷Ņµ±¾ĻµĮŠ“š°ø Źī¼Ł½ÓĮ¦ČüŠĀ½®ĒąÉŁÄź³ö°ęÉēĻµĮŠ“š°ø
Źī¼Ł½ÓĮ¦ČüŠĀ½®ĒąÉŁÄź³ö°ęÉēĻµĮŠ“š°ø