题目内容
已知关于 的方程:
的方程: ①和
①和 ②,其中
②,其中 .
.
(1)求证:方程①总有两个不相等的实数根;
(2)设二次函数 的图象与
的图象与 轴交于
轴交于 、
、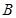 两点(点
两点(点 在点
在点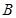 的左侧),将
的左侧),将 、
、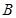 两点按照相同的方式平移后,点
两点按照相同的方式平移后,点 落在点
落在点 处,点
处,点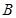 落在点
落在点 处,若点
处,若点 的横坐标恰好是方程②的一个根,求
的横坐标恰好是方程②的一个根,求 的值;
的值;
(3)设二次函数 ,在(2)的条件下,函数
,在(2)的条件下,函数 ,
, 的图象位于直线
的图象位于直线 左侧的部分与直线
左侧的部分与直线 (
( )交于两点,当向上平移直线
)交于两点,当向上平移直线 时,交点位置随之变化,若交点间的距离始终不变,则
时,交点位置随之变化,若交点间的距离始终不变,则 的值是________________.
的值是________________.

 的方程:
的方程: ①和
①和 ②,其中
②,其中 .
.(1)求证:方程①总有两个不相等的实数根;
(2)设二次函数
 的图象与
的图象与 轴交于
轴交于 、
、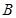 两点(点
两点(点 在点
在点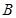 的左侧),将
的左侧),将 、
、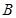 两点按照相同的方式平移后,点
两点按照相同的方式平移后,点 落在点
落在点 处,点
处,点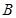 落在点
落在点 处,若点
处,若点 的横坐标恰好是方程②的一个根,求
的横坐标恰好是方程②的一个根,求 的值;
的值;(3)设二次函数
 ,在(2)的条件下,函数
,在(2)的条件下,函数 ,
, 的图象位于直线
的图象位于直线 左侧的部分与直线
左侧的部分与直线 (
( )交于两点,当向上平移直线
)交于两点,当向上平移直线 时,交点位置随之变化,若交点间的距离始终不变,则
时,交点位置随之变化,若交点间的距离始终不变,则 的值是________________.
的值是________________.
(1)证明见解析;(2)3;(3)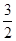 .
.
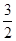 .
.试题分析:(1)证明方程根的判别式大于0即可.
(2)根据平移的性质,得到点
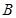 平移后的坐标
平移后的坐标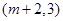 ,由点
,由点 的横坐标恰好是方程②的一个根,代入求解即可.
的横坐标恰好是方程②的一个根,代入求解即可.(3)求出过两抛物线的顶点的直线的
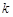 即为所求.
即为所求.试题解析:(1)
 ,
,由
 知必有
知必有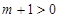 ,故
,故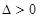 .
.∴方程①总有两个不相等的实数根.
(2)令
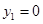 ,依题意可解得
,依题意可解得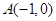 ,
,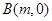 .
.∵平移后,点
 落在点
落在点 处,
处,∴平移方式是将点
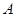 向右平移2个单位,再向上平移3个单位得到.
向右平移2个单位,再向上平移3个单位得到.∴点
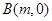 按相同的方式平移后,点
按相同的方式平移后,点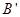 为
为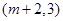 .
.则依题意有
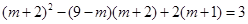 .
.解得
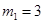 ,
,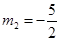 (舍负).
(舍负).∴
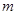 的值为3.
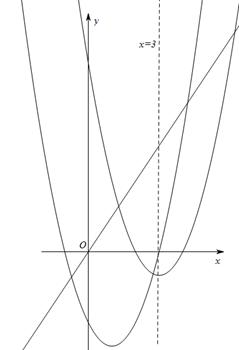
的值为3.(3)在(2)的条件下,
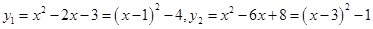 ,
,两抛物线的顶点坐标分别为
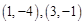 ,则过这两点的直线解析式为
,则过这两点的直线解析式为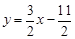 .
.∴
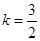 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 的顶点坐标为 .
的顶点坐标为 .

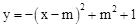 有最大值4,则实数m的值为( )
有最大值4,则实数m的值为( )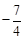 (B)
(B)  或
或 (c)2或
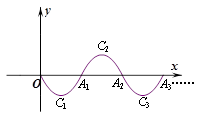
(c)2或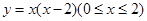 的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .
的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .