Question

【题目】已知二次函数y＝ax2+bx+c的图象过点A（1，0），B（﹣3，0），C（0，﹣3）三点．

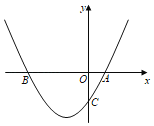
（1）求这个二次函数的解析式．

（2）在抛物线上存在一点P使△ABP的面积为10，求点P的坐标．（写出详细的解题过程）

Answer 1

【答案】（1）y＝x2+2x﹣3；（2）P（﹣4，5）或P（2，5）．

【解析】

（1）设交点式y=a（x-1）（x+3），然后把C（0，-3）代入求出a的值即可；

（2）首先算出AB的长，再设P（m，n），根据△ABP的面积为10可以计算出n的值，然后再利用二次函数解析式计算出m的值即可得到P点坐标．

（1）设抛物线解析式为y＝a（x﹣1）（x+3），

把C（0，﹣3）代入得a（﹣1）3＝﹣3，解得a＝1，

所以抛物线解析式为y＝（x﹣1）（x+3），即y＝x2+2x﹣3；

（2）∵A（1，0），B（﹣3，0），

∴AB＝4，

设P（m，n），

∵△ABP的面积为10，

∴AB|n|＝10，

解得：n＝±5，

当n＝5时，m2+2m﹣3＝5，

解得：m＝﹣4或2，

∴P（﹣4，5）或P（2，5）；

当n＝﹣5时，m2+2m﹣3＝﹣5，即m2+2m+2＝0，

∵△＝22﹣4×1×2＜0，

∴n＝﹣5不存在，

故P（﹣4，5）或P（2，5）．