题目内容
抛物线y=mx2+x和y=nx2+x与x轴正半轴分别交于点A和点B.若点A在点B的右边,则m与n的大小关系为
- A.m>n
- B.m<n
- C.m=n
- D.无法确定
A
分析:先设点A和点B的坐标分别为(a,0)、(b,0),且a>b>0,再把两点坐标分别代入抛物线y=mx2+x和y=nx2+x,用a、b表示出m、n的值.再根据不等式的基本性质即可解答.
解答:设点A和点B的坐标分别为(a,0)、(b,0),且a>b>0,
则ma2+a=0,nb2+b=0,即a(am+1)=0,b(bm+1)=0,
∵a>b>0,
∴am+1=0,bm+1=0,解得m=- ,n=-
,n=- ,
,
∵a>b,
∴- >-
>- ,即m>n.
,即m>n.
故选A.
点评:本题考查的是二次函数的图象与x轴的交点问题及不等式的基本性质,解答此题的关键是熟知不等式与x轴交点的坐标特点.
分析:先设点A和点B的坐标分别为(a,0)、(b,0),且a>b>0,再把两点坐标分别代入抛物线y=mx2+x和y=nx2+x,用a、b表示出m、n的值.再根据不等式的基本性质即可解答.
解答:设点A和点B的坐标分别为(a,0)、(b,0),且a>b>0,
则ma2+a=0,nb2+b=0,即a(am+1)=0,b(bm+1)=0,
∵a>b>0,
∴am+1=0,bm+1=0,解得m=-
 ,n=-
,n=- ,
,∵a>b,
∴-
 >-
>- ,即m>n.
,即m>n.故选A.
点评:本题考查的是二次函数的图象与x轴的交点问题及不等式的基本性质,解答此题的关键是熟知不等式与x轴交点的坐标特点.

练习册系列答案
相关题目
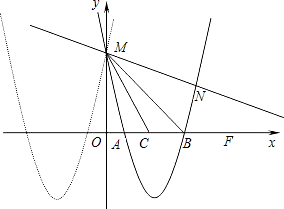 如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B.
如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B. (2012•顺义区一模)如图,在平面直角坐标系xOy中,抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3),
(2012•顺义区一模)如图,在平面直角坐标系xOy中,抛物线y=mx2+2mx+n经过点A(-4,0)和点B(0,3),