题目内容
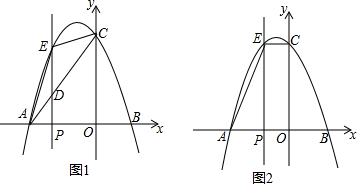
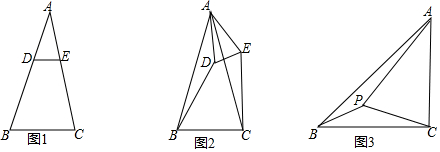
5.已知:在△ABC中,AB=AC.(1)特殊情形:如图1,当DE∥BC时,求证:DB=EC.
(2)发现探究:若将图1中的△ADE绕点A逆时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)实际运用:如图3,某小区在A、B、C三幢楼之间有一片等腰直角三角形的绿地,为了方便居民之间的沟通和休闲,决定在绿地上建造一个休闲亭P,使它到A楼的距离为30m,到B楼的距离为10m,到C楼的距离为20m.建好后,住在该小区的初二学生小明通过计算得到∠BPC刚好等于135°,聪明的你知道为什么吗?请说明理由.
分析 (1)由DE∥BC,得到 $\frac{DB}{AB}$=$\frac{EC}{AC}$,结合AB=AC,得到DB=EC;
(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;
(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
解答 (1)证明:如图1中,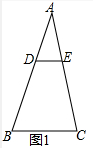
∵DE∥BC,
∴$\frac{DB}{AB}$=$\frac{EC}{AC}$,
∵AB=AC,
∴DB=EC,
(2)解:成立.
理由:如图2中,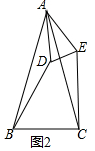
由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中
$\left\{\begin{array}{l}{AD=AE}\\{∠DAB=∠EAC}\\{AB=AC}\end{array}\right.$,
∴△DAB≌△EAC,
∴DB=CE,
(3)如图,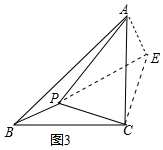
将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=20,AE=BP=10,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2 0$\sqrt{2}$,
在△PEA中,PE2=(2 0$\sqrt{2}$)2=800,AE2=102=100,PA2=302=900,
∵PE2+AE2=AP2,
∴△PEA是直角三角形
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA
∴∠BPC=∠CEA=135°.
点评 此题是几何变换综合题,主要考查了旋转的性质,平行线的性质,全等三角形的性质和判定,勾股定理及其逆定理,解本题的关键是构造全等三角形,也是本题的难点.

练习册系列答案
相关题目
16.点M(x,y)在第四象限,且|x|=3,|y|=2,则点M的坐标是( )
| A. | (-3,2) | B. | (-3,-2) | C. | (-2,-3) | D. | (3,-2) |
13.在“阳光体育节”活动中,某校对六(1)班、(2)班同学各50人参加体育活动的情况进行了调查,结果如图所示.下列说法中( )是正确的.
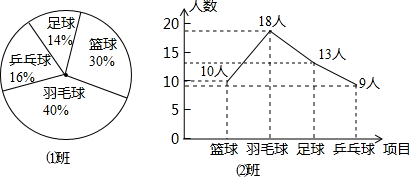

| A. | 喜欢乒乓球的人数(1)班比(2)班多 | B. | 喜欢足球的人数(1)班比(2)班多 | ||
| C. | 喜欢羽毛球的人数(1)班比(2)班多 | D. | 喜欢篮球的人数(2)班比(1)班多 |
14.计算5a-a结果正确的是( )
| A. | 4a | B. | 5 | C. | -4 | D. | -4a |
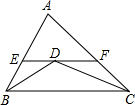 如图,△ABC中,AB=8,AC=10,BD,CD分别平分∠ABC,∠ACB交于点D,过点D作直线平行于BC,交AB,AC于E,F,则△AEF的周长为( )
如图,△ABC中,AB=8,AC=10,BD,CD分别平分∠ABC,∠ACB交于点D,过点D作直线平行于BC,交AB,AC于E,F,则△AEF的周长为( )