题目内容
 如图所示,将一副三角尺摆放在一起,连接AD,求∠ADB的余切值.
如图所示,将一副三角尺摆放在一起,连接AD,求∠ADB的余切值.分析:先过点A作DB的延长线的垂线AA’,设BD=DC=1,求出BC的长,在Rt△ABC中,根据∠ACB=30°,求出AB的长,在Rt△AA’B中,求出∠ABA’=180°-(∠DBC+∠ABC)=45°,
得出BA’=AA’=AB•sin45°=
,DA’=BD+A’B=
+1,最后根据cot∠ADB=
即可得出答案.
得出BA’=AA’=AB•sin45°=
| ||
| 3 |
| ||
| 3 |
| DA′ |
| AA′ |
解答: 解:过点A作DB的延长线的垂线AA’,垂足为A’,
解:过点A作DB的延长线的垂线AA’,垂足为A’,
在等腰Rt△BDC中,∠DBC=45°,设BD=DC=1,则BC=
,
在Rt△ABC中,∠ACB=30°,则AB=BC•tan30°=
,
在Rt△AA’B中,∠ABA’=180°-(∠DBC+∠ABC)=45°,
则BA’=AA’=AB•sin45°=
,
在Rt△AA’D中,DA’=BD+A’B=
+1,
则cot∠ADB=
=
=
+1.
 解:过点A作DB的延长线的垂线AA’,垂足为A’,
解:过点A作DB的延长线的垂线AA’,垂足为A’,在等腰Rt△BDC中,∠DBC=45°,设BD=DC=1,则BC=
| 2 |
在Rt△ABC中,∠ACB=30°,则AB=BC•tan30°=
| ||
| 3 |
在Rt△AA’B中,∠ABA’=180°-(∠DBC+∠ABC)=45°,
则BA’=AA’=AB•sin45°=
| ||
| 3 |
在Rt△AA’D中,DA’=BD+A’B=
| ||
| 3 |
则cot∠ADB=
| DA′ |
| AA′ |
| ||||
|
| 3 |
点评:此题考查了解直角三角形,关键是根据题意做出辅助线,构造出直角三角形,用到的知识点是锐角三角函数的定义.

练习册系列答案
相关题目
 如图所示,将一副三角尺拼成一起,则∠ABD=
如图所示,将一副三角尺拼成一起,则∠ABD=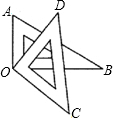 (1)如图所示,将一副三角尺的直角顶点重合在点O处.
(1)如图所示,将一副三角尺的直角顶点重合在点O处.
 (1)如图所示,将一副三角尺的直角顶点重合在点O处.
(1)如图所示,将一副三角尺的直角顶点重合在点O处.
 如图所示,将一副三角尺摆放在一起,连接AD,求∠ADB的余切值.
如图所示,将一副三角尺摆放在一起,连接AD,求∠ADB的余切值.