题目内容
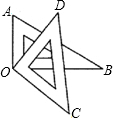 (1)如图所示,将一副三角尺的直角顶点重合在点O处.
(1)如图所示,将一副三角尺的直角顶点重合在点O处.①∠AOD和∠BOC相等吗?说明理由.
②∠AOC和∠BOD在数量上有何关系?试写一个关系式.
(2)如图,已知线段AB=6,延长线段AB到C,使BC=2AB,点D是AC的中点,
求①AC的长;②BD的长.
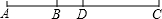
分析:(1)①由直角的定义和等量代换证得∠AOD和∠BOC相等;②根据两直角∠AOB+∠COD=180°可以推知∠AOC+∠BOD=180°;
(2)①根据已知条件和图示易得AC=AB+BC=3AB;②根据图示易求BD=AD-AB.
(2)①根据已知条件和图示易得AC=AB+BC=3AB;②根据图示易求BD=AD-AB.
解答:解:(1)①相等.
证明:∵∠AOD+∠DOB=90°,∠BOC+∠DOB=90°,
∴∠AOD=∠BOC;
②∠AOC+∠BOD=180°;
(2)①AC=AB+BC=3AB=3×6=18;
②BD=AD-AB=
AC-AB=
×18-6=3.
证明:∵∠AOD+∠DOB=90°,∠BOC+∠DOB=90°,
∴∠AOD=∠BOC;
②∠AOC+∠BOD=180°;
(2)①AC=AB+BC=3AB=3×6=18;
②BD=AD-AB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了角的计算、两点间的距离.解答该题的关键是根据图示提取与解题有关的信息,需要学生有一定的读图能力.

练习册系列答案
相关题目
 27、如图所示,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G,若∠EFG=50°,求∠1,∠2的度数.
27、如图所示,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G,若∠EFG=50°,求∠1,∠2的度数. …
… 如图所示,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在外面的长为hcm,则h的取值范围是( )
如图所示,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在外面的长为hcm,则h的取值范围是( )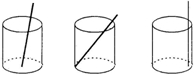 如图所示,将一根长24cm的筷子,置于底面直径为9cm,高为12cm的圆柱形水杯中,如图,设筷子露出在杯子外面的部分长为hcm,则h的取值范围是
如图所示,将一根长24cm的筷子,置于底面直径为9cm,高为12cm的圆柱形水杯中,如图,设筷子露出在杯子外面的部分长为hcm,则h的取值范围是