题目内容
用正三角形和正六边形镶嵌,若每一个顶点周围有m个正三角形、n个正六边形,则m,n满足的关系式是
- A.2m+3n=12
- B.m+n=8
- C.2m+n=6
- D.m+2n=6
D
分析:正多边形的组合能否进行平面镶嵌,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明可以进行平面镶嵌;反之,则说明不能进行平面镶嵌.
解答:正多边形的平面镶嵌,每一个顶点处的几个角之和应为360度,
而正三角形和正六边形内角分别为60°、120°,
根据题意可知60°×m+120°×n=360°,
化简得到m+2n=6.
故选D.
点评:解决此类题,可以记住几个常用正多边形的内角,及能够用两种正多边形镶嵌的几个组合.
分析:正多边形的组合能否进行平面镶嵌,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明可以进行平面镶嵌;反之,则说明不能进行平面镶嵌.
解答:正多边形的平面镶嵌,每一个顶点处的几个角之和应为360度,
而正三角形和正六边形内角分别为60°、120°,
根据题意可知60°×m+120°×n=360°,
化简得到m+2n=6.
故选D.
点评:解决此类题,可以记住几个常用正多边形的内角,及能够用两种正多边形镶嵌的几个组合.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
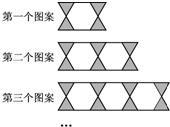 17、用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n个图案中正三角形的个数为
17、用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n个图案中正三角形的个数为