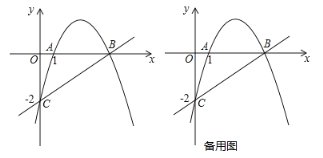
题目内容
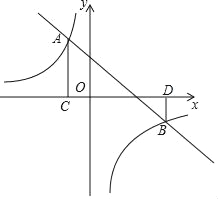
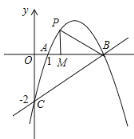
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,且点
,且点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() .
.
(1)求这条抛物线的解析式;
(2)若在![]() 轴上方的抛物线上有点
轴上方的抛物线上有点![]() ,使
,使![]() 的内心恰好在
的内心恰好在![]() 轴上,求此时
轴上,求此时![]() 的面积;
的面积;
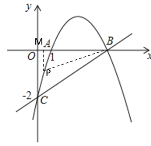
(3)在直线![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() ,过
,过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() 是否存在
是否存在![]() 点,使得以
点,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出符合条件的点
相似?若存在,请求出符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)4;(3)存在,点
;(2)4;(3)存在,点![]() 为
为![]() .
.
【解析】
(1)将点A、B的坐标代入并结合对称轴公式即可求出二次函数的解析式;
(2)根据三角形内心的性质可得x轴平分![]() ,设
,设![]() 交
交![]() 轴于
轴于![]() 点,利用ASA证出△EBO≌△CBO,即可求出点E的坐标,然后根据对称性求出点B的坐标,利用待定系数法即可求出直线BD的解析式,联立方程即可求出点D的坐标,根据三角形中线的性质即可求出结论;
点,利用ASA证出△EBO≌△CBO,即可求出点E的坐标,然后根据对称性求出点B的坐标,利用待定系数法即可求出直线BD的解析式,联立方程即可求出点D的坐标,根据三角形中线的性质即可求出结论;
(3)设![]() 点的横坐标为
点的横坐标为![]() ,则
,则![]() 点的纵坐标为:
点的纵坐标为:![]() ,然后根据点P的位置分类讨论,在每种情况下根据相似三角形的对应情况分类讨论,分别画出对应的图形,根据相似三角形的性质即可求出结论.
,然后根据点P的位置分类讨论,在每种情况下根据相似三角形的对应情况分类讨论,分别画出对应的图形,根据相似三角形的性质即可求出结论.
解:(1)由题意可得
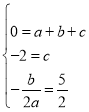
解得: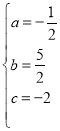
∴这条抛物线的解析式为![]() ;
;
(2)![]() 的内心在
的内心在![]() 轴上,
轴上,
![]() 轴平分
轴平分![]() ,设
,设![]() 交
交![]() 轴于
轴于![]() 点,
点,
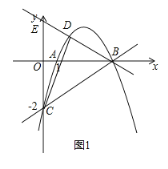
∴∠EBO=∠CBO,
∵BO=BO,∠BOE=∠BOC=90°
∴△EBO≌△CBO
∴OE=OC=2
则![]() ,
,
∵![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]()
∴点B的坐标为(4,0)
设直线BD的解析式为![]()
将点B和点E的坐标代入,得
![]()
解得: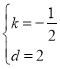
所以![]() 直线为
直线为![]() ,
,
联立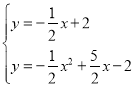
解得:![]() 或
或![]() ,其中(4,0)为点B的坐标
,其中(4,0)为点B的坐标
![]() ,
,
∴此时![]() 为
为![]() 的中点,
的中点,
![]() .
.
(3)存在,设![]() 点的横坐标为
点的横坐标为![]() ,则
,则![]() 点的纵坐标为:
点的纵坐标为:![]()
当![]() 时,
时,![]() ,
,
![]() ,
,
①当![]() 时,
时,
∴![]()
即![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
![]() ;
;
②当![]() 时,
时,
![]() ,
,
即![]() ,
,
解得![]() ,
,![]() (均不合题意,舍去),
(均不合题意,舍去),
当0<![]() 时,
时,![]()
③∵∠OAC>∠OBC>∠MBO
∴不存在点P,使![]()
④当![]() 时,
时,
![]()
![]()
解得:解得![]() ,
,![]() (均不合题意,舍去),
(均不合题意,舍去),
综上所述,符合条件的点![]() 为
为![]() .
.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案【题目】某生产商存有1200千克![]() 产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产
产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产![]() 产品,
产品,![]() 产品售价为200元/千克.经市场调研发现,
产品售价为200元/千克.经市场调研发现,![]() 产品存货的处理价格
产品存货的处理价格![]() (元/千克)与处理数量
(元/千克)与处理数量![]() (千克)满足一次函数关系(
(千克)满足一次函数关系(![]() ),且得到表中数据.
),且得到表中数据.
|
|
200 | 350 |
400 | 300 |
(1)请求出处理价格![]() (元千克)与处理数量
(元千克)与处理数量![]() (千克)之间的函数关系;
(千克)之间的函数关系;
(2)若![]() 产品生产成本为100元千克,
产品生产成本为100元千克,![]() 产品处理数量为多少千克时,生产
产品处理数量为多少千克时,生产![]() 产品数量最多,最多是多少?
产品数量最多,最多是多少?
(3)由于改进技术,![]() 产品的生产成本降低到了
产品的生产成本降低到了![]() 元/千克,设全部产品全部售出,所得总利润为
元/千克,设全部产品全部售出,所得总利润为![]() (元),若
(元),若![]() 时,满足
时,满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围.
的取值范围.