题目内容
【题目】已知抛物线
若该抛物线经过点
，试求
的值及抛物线的顶点坐标．
求此抛物线的顶点坐标(用含的代数式表示) ，并证明：不论为何值，该抛物线的顶点都在同一条直线
上．
直线截抛物线所得的线段长是否为定值?若是，请求出这个定值；若不是，请说明理由．
【答案】（1）当
时，
，其顶点坐标为
，当
时，
，其顶点坐标为
；（2）顶点坐标为
；证明见解析；（3）是，
【解析】
（1）将点P的坐标代入抛物线解析式中可求出m的值，再利用二次函数的性质可求出抛物线的顶点坐标；
（2）利用配方法找出抛物线的顶点坐标，由其纵坐标减横坐标为定值，可得出不论m为何值，该抛物线的顶点坐标都在同一条直线l上；
（3）将直线l的解析式代入抛物线解析式中可得出关于x的一元二次方程，解之可得出交点的横坐标，利用一次函数图象上点的坐标特征可得出交点的坐标，再利用两点间的距离公式可求出直线l截抛物线所得的线段长．
解：
将
代入
得
解得或
当时， ，其顶点坐标为
当时， ，其顶点坐标为
方法1：设顶点坐标为
则
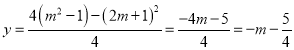
顶点坐标为
方法2：
∵
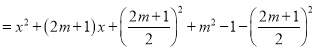
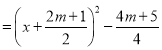
顶点坐标为
证明：∵
不论
为何值，该抛物线的顶点都在同一条直线
上
是
将
代入得
与抛物线的交点坐标分别为
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
