题目内容
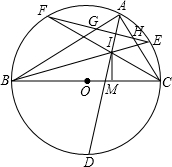 如图,I为△ABC的内心,△ABC的外接圆O,O在BC上,AD、BE、CF都经过I点分别交⊙O于点D、E、F,EF交AB于点G,交AC于点H,IM⊥BC于M.则下列结论:①EF⊥AD;②AB+AC-BC=
如图,I为△ABC的内心,△ABC的外接圆O,O在BC上,AD、BE、CF都经过I点分别交⊙O于点D、E、F,EF交AB于点G,交AC于点H,IM⊥BC于M.则下列结论:①EF⊥AD;②AB+AC-BC=| 2 |
③AD=
| 2 |
| 1 |
| 2 |
| A、①②④ | B、①② |
| C、①②③ | D、③④ |
分析:根据内心的定义得到∠ABE=∠CBE,∠ACF=∠BCF,∠BAD=∠CAD,求出∠EAD+∠AEF=90°即可判断①;求出三角形内切圆的半径是
(AC+AB-BC),根据勾股定理求出AI=
IH即可判断②;求出AD=AI+ID=
(AC+AB),求出
(IM+
BC)=
(AC+AB),即可判断③;根据相似三角形的性质即可判断④.
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解答:解:∵I为△ABC的内心,
∴∠ABE=∠CBE,∠ACF=∠BCF,∠BAD=∠CAD,
∴弧AE+弧AF+弧CD=180°,
∴∠AGF=∠EAD+∠AEF=90°,∴①正确;
∵O在BC上,
∴∠BAC=90°,
∵I是△ABC的内心,
∴CM=BM,CQ=CM,BM=BH,
∴∠IQA=∠CAB=∠IHA=90°,IQ=IH,
∴四边形QIHA是正方形,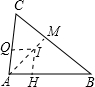
∴IQ=AQ=AI=IH,
∴AC-IH+AB-IH=BC,
∴IH=
(AC+AB-BC),
由勾股定理得:AI=
IH,
∴②正确;
AD=AI+ID=
(AC+AB-BC)+
BC,
=
AC+
AB,
(IM+
BC)=
[
(AC+AB-BC)+
BC]=
AC+
AB,
∴③正确;
∵∠F=∠EBC,∠FEI=∠ICM,
∴△EFI∽△CBI,
∴
=(
)2,
∵BC一定,
∴④错误;
故选C.
∴∠ABE=∠CBE,∠ACF=∠BCF,∠BAD=∠CAD,
∴弧AE+弧AF+弧CD=180°,
∴∠AGF=∠EAD+∠AEF=90°,∴①正确;
∵O在BC上,
∴∠BAC=90°,
∵I是△ABC的内心,
∴CM=BM,CQ=CM,BM=BH,
∴∠IQA=∠CAB=∠IHA=90°,IQ=IH,
∴四边形QIHA是正方形,

∴IQ=AQ=AI=IH,
∴AC-IH+AB-IH=BC,
∴IH=
| 1 |
| 2 |
由勾股定理得:AI=
| 2 |
∴②正确;
AD=AI+ID=
| 1 | ||
|
| ||
| 2 |
=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴③正确;
∵∠F=∠EBC,∠FEI=∠ICM,
∴△EFI∽△CBI,
∴
| S△BIC |
| S△EIF |
| BC |
| EF |
∵BC一定,
∴④错误;
故选C.
点评:本题主要考查对三角形的内切圆与内心,三角形的外角性质,相似三角形的性质,圆周角定理,切线长定理,正方形的性质和判定等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
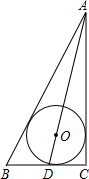 如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )
如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
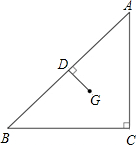 如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )
如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )| A、7 | ||
B、14
| ||
C、
| ||
D、
|
 6、如图,⊙O为△ABC的外接圆,BC为直径,AC=AB,则∠D的度数为( )
6、如图,⊙O为△ABC的外接圆,BC为直径,AC=AB,则∠D的度数为( ) 25、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,那么BE⊥AC吗?为什么?
25、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,那么BE⊥AC吗?为什么?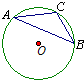 5、如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=
5、如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=