题目内容
 如图,已知AC、BD相交于点0,AO=DO,BO=CO.
如图,已知AC、BD相交于点0,AO=DO,BO=CO.求证:(1)△ABO≌△DCO;
(2)△ABC≌△DCB.
考点:全等三角形的判定
专题:证明题
分析:(1)利用“SAS”可证明△ABO≌△DCO;
(2)先利用OB=OC得到∠OBC=∠OCB,然后根据“SAS”可证明△ABC≌△DCB.
(2)先利用OB=OC得到∠OBC=∠OCB,然后根据“SAS”可证明△ABC≌△DCB.
解答:证明:(1)在△ABO和△DCO中,
,
∴△ABO≌△DCO(SAS);
(2)∵OB=OC,
∴∠OBC=∠OCB,
∵AO=DO,BO=CO,
∴AC=BD,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS).
|
∴△ABO≌△DCO(SAS);
(2)∵OB=OC,
∴∠OBC=∠OCB,
∵AO=DO,BO=CO,
∴AC=BD,
在△ABC和△DCB中,
|
∴△ABC≌△DCB(SAS).
点评:本题考查了全等三角形的判定:可利用”SSS”、“SAS”、“ASA”、“AAS”判断两三角形全等.

练习册系列答案
相关题目
已知实数a、b、c满足a<0,4a-2b+c>0,则一定有( )
| A、b2-4ac>0 |
| B、b2-4ac<0 |
| C、b2-4ac≥0 |
| D、b2-4ac≤0 |
一辆汽车以50km/h的速度行驶,行驶的路程s(km)与行驶的时间t(h)之间的关系式为s=50t,其中变量是( )
| A、速度与路程 |
| B、速度与时间 |
| C、路程与时间 |
| D、三者均为变量 |
 7、如图:数轴上表示1、
7、如图:数轴上表示1、| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、2-
|
 如图,已知AD是Rt△ABC斜边BC边上的高,则图中有几对相似三角形( )
如图,已知AD是Rt△ABC斜边BC边上的高,则图中有几对相似三角形( )| A、1对 | B、2对 | C、3对 | D、4对 |
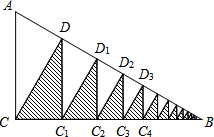 如图,已知Rt△ABC中,∠B=30°,AC=2,作△CDB的高DC1,作△DC1B的高C1D1,…,就这样无限作下去,求图中阴影部分的面积.
如图,已知Rt△ABC中,∠B=30°,AC=2,作△CDB的高DC1,作△DC1B的高C1D1,…,就这样无限作下去,求图中阴影部分的面积.