题目内容
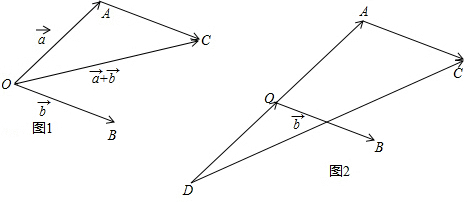
如图，
，
是以点O为起点的两个非零向量，且|
|=|
|=|
-
|=
，在图中作
+
，2
+
，并求
+
的模长．
| a |
| b |
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| a |
| b |
| a |
| b |
如图1：过点A作
=
，
连接OC，
则
=
+
，
即为所求；
如图2，作
=
，
过点A作
=
，
连接DC，
则
=2
+
，
即为所求；
连接AB，
则
=
-
，
∵|
|=|
|=|
-
|=
，
∴OA=OB=AB=
，
∴∠AOB=60°，
∵
=
，
∴AC∥OB，AC=OB，
∴∠C=∠COB，
∵OA=OB，
∴OA=OC，
∴∠C=∠AOC，
∴∠AOC=∠COB=
∠AOB=30°，
∴OD⊥AB，
∴OD=OA•cos∠AOD=
×
=
，CD=AC•cos∠C=
×
=
，
∴OC=3，
∴
+
的模长为3．
| AC |
| b |
连接OC，
则
| OC |
| a |
| b |
| OC |
如图2，作
| DO |
| a |
过点A作
| AC |
| b |
连接DC，
则
| DC |
| a |
| b |
| DC |
连接AB，
则
| AB |
| b |
| a |
∵|
| a |
| b |
| a |
| b |
| 3 |
∴OA=OB=AB=
| 3 |
∴∠AOB=60°，
∵
| AC |
| OB |
∴AC∥OB，AC=OB，
∴∠C=∠COB，
∵OA=OB，
∴OA=OC，
∴∠C=∠AOC，
∴∠AOC=∠COB=
| 1 |
| 2 |
∴OD⊥AB，
∴OD=OA•cos∠AOD=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴OC=3，
∴
| a |
| b |
练习册系列答案
阅读快车系列答案
相关题目
分别与x、y轴交于A 
、B两点，过点B的直线交x轴负半轴于C，且
；
（
）交AB于E，交BC于点F，交x轴于D，是否存在这样的直线EF，使得
？若存在，求出
的值；若不存在，说明理由？
