题目内容
如图所示,已知 ,
, 为反比例函数
为反比例函数 图像上的两点,动点
图像上的两点,动点 在
在 正半轴上运动,当线段
正半轴上运动,当线段 与线段
与线段 之差达到最大时,点
之差达到最大时,点 的坐标是( )
的坐标是( )
A. | B. | C. | D. |
D
解析试题分析:先求出A、B的坐标,再根据待定系数法求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,  ,延长AB交x轴于P′,当P在P′点时,
,延长AB交x轴于P′,当P在P′点时, ,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
由 ,
, 为反比例函数
为反比例函数 图像上的两点,
图像上的两点,
可得A( ,2),B(2,
,2),B(2, ),
),
∵在△ABP中, ,
,
∴延长AB交x轴于P′,当P在P′点时, ,
,
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
∵图象过点A( ,2),B(2,
,2),B(2, ),
), ,解得
,解得 ,
,
∴直线AB的解析式是 ,
,
当 时,
时, ,
,
即P ,
,
故选D.
考点:本题考查的是三角形的三边关系,用待定系数法求一次函数的解析式
点评:解答本题的关键是熟练掌握三角形的三边关系:三角形的任两边之和大于第三边;本题中确定P点的位置是突破口.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质: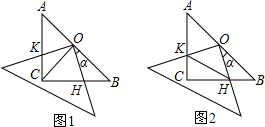

 在八年级上册我们已经知道三角形的中位线具有如下性质:
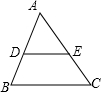
在八年级上册我们已经知道三角形的中位线具有如下性质: BC;④DE∥BC.
BC;④DE∥BC.