题目内容
11.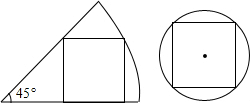 把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )| A. | 4:5 | B. | 2:5 | C. | $\sqrt{5}$:2 | D. | $\sqrt{5}$:$\sqrt{2}$ |
分析 首先分别求出扇形和圆的半径,再根据面积公式求出面积,最后求出比值即可.
解答 解:如图1,连接OD,
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=90°,AB=BC=CD=1,
∵∠AOB=45°,
∴OB=AB=1,
由勾股定理得:OD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,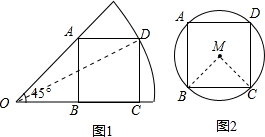
∴扇形的面积是$\frac{45π×(\sqrt{5})^{2}}{360}$=$\frac{5}{8}$π;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=90°,MB=MC,
∴∠MCB=∠MBC=45°,
∵BC=1,
∴MC=MB=$\frac{\sqrt{2}}{2}$,
∴⊙M的面积是π×($\frac{\sqrt{2}}{2}$)2=$\frac{1}{2}$π,
∴扇形和圆形纸板的面积比是$\frac{5}{8}$π÷($\frac{1}{2}$π)=$\frac{5}{4}$,
即圆形纸片和扇形纸片的面积比是4:5.
故选A.
点评 本题考查了正方形性质,圆内接四边形性质,扇形的面积公式的应用,解此题的关键是求出扇形和圆的面积,题目比较好,难度适中.

练习册系列答案
相关题目
1.4x2+49y2配成完全平方式应加上( )
| A. | 14xy | B. | -14xy | C. | ±28xy | D. | 0 |
16.下列事件是随机事件的是( )
| A. | 晴天的早晨,太阳从东方升起 | |
| B. | 测量某天的最低气温,结果为-150℃ | |
| C. | 打开数学课本时刚好翻到第60页 | |
| D. | 在一次体育考试中,小王跑100米用了4秒钟 |
20.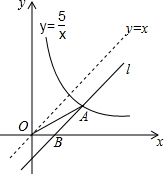 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )
如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )
 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )
如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )| A. | 5 | B. | 10 | C. | 15 | D. | 25 |
1.设a=$\sqrt{11}$+1,a在两个相邻整数之间,则这两个整数是( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
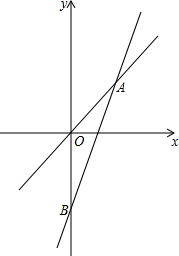 如图,已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB
如图,已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB 如图,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,若AB=24,则CD的长是12.
如图,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,若AB=24,则CD的长是12.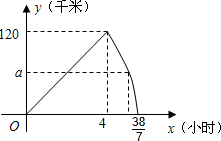 甲、乙两车同时从A地出发,以各自的速度向B地行驶,甲车先到达B地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
甲、乙两车同时从A地出发,以各自的速度向B地行驶,甲车先到达B地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示. 如图,请你把图形分成面积相等的两部分(不写作法,保留作图痕迹)
如图,请你把图形分成面积相等的两部分(不写作法,保留作图痕迹)