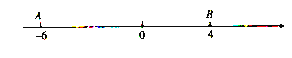题目内容
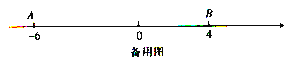
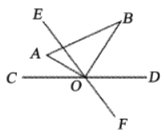
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,将一直角三角尺
,将一直角三角尺![]() 的直角顶点与点
的直角顶点与点![]() 重合,
重合,![]() 平分
平分![]() .
.
(1)![]() 的度数为______________
的度数为______________![]() ;
;
(2)将三角尺![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,同时直线
顺时针旋转,同时直线![]() 也以每秒
也以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,设运动时间为
顺时针旋转,设运动时间为![]() 秒
秒![]() .
.
①求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() ;
;
②求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() .
.
【答案】(1)60;(2)①t=2.5s或32.5s;②t=12s或36s.
【解析】
(1)根据角平分线的定义,即可求出∠COA,然后根据平角的定义即可求出![]() ;
;
(2)①根据直线EF平分∠AOB,分OE平分∠AOB和OF平分∠AOB两种情况,分别列出方程即可求出t;
②根据直线EF平分![]() ,分OE平分
,分OE平分![]() 和OF平分
和OF平分![]() 两种情况,分别列出方程即可求出t;
两种情况,分别列出方程即可求出t;
解:(1)∵![]() ,
,![]() 平分
平分![]()
∴∠COA=∠AOE=![]()
∵∠AOB=90°
∴![]() =180°-∠COA-∠AOB=60°
=180°-∠COA-∠AOB=60°
故答案为:60°;
(2)∠COF=180°-∠COE=120°
∴∠AOF=∠COE+∠AOC=150°
①直线EF平分∠AOB,分两种情况:
(i)当OE平分∠AOB时,∠AOE=45°,
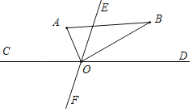
即9t+30°-3t=45°,
解得t=2.5;
(ii)当OF平分∠AOB时,∠AOF=45°,
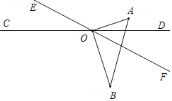
即9t﹣150°﹣3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②直线EF平分∠BOD,分两种情况:
(i)当OE平分∠BOD时,∠BOE=![]() ∠BOD,
∠BOD,
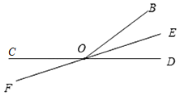
即9t﹣60°﹣3t=![]() (60°﹣3t),
(60°﹣3t),
解得t=12;
当OF平分∠BOD时,∠DOF=![]() ∠BOD,
∠BOD,
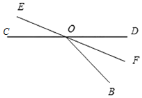
即3t﹣(9t﹣240°)=![]() (3t﹣60°),
(3t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目