题目内容
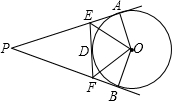 如图,已知:PA、PB、EF 分别切⊙O 于A、B、D,若PA=10cm,那么△PEF 周长是
如图,已知:PA、PB、EF 分别切⊙O 于A、B、D,若PA=10cm,那么△PEF 周长是分析:根据切线长定理即可证得△PEF 周长等于2PA即可求解;根据切线的性质以及四边形的内角和定理即可求得∠AOB的度数,然后根据∴∠EOF=
∠AOB即可求解.
| 1 |
| 2 |
解答:解:∵PA、PB、EF 分别切⊙O 于A、B、D.
∴AE=ED,DF=FR
∴△PEF 周长是PE+PF+EF=PE+EA+PF+FR=PA+PR=2PA=20cm;
∵PA、PB、EF 分别切⊙O 于A、B
∴∠PAO=∠PRO=90°
∴∠AOB=360°=90°-90°-35°=145°;
∴∠EOF=
∠AOB=72.5°
故答案是:20°,145°,72.5°.
∴AE=ED,DF=FR
∴△PEF 周长是PE+PF+EF=PE+EA+PF+FR=PA+PR=2PA=20cm;
∵PA、PB、EF 分别切⊙O 于A、B
∴∠PAO=∠PRO=90°
∴∠AOB=360°=90°-90°-35°=145°;
∴∠EOF=
| 1 |
| 2 |
故答案是:20°,145°,72.5°.
点评:本题主要考查了切线长定理,正确理解图形中的线段与角之间的关系是解题的关键.

练习册系列答案
相关题目
 连接CE并延长,交⊙O于F,连接AF.
连接CE并延长,交⊙O于F,连接AF. m>n)的图象.
m>n)的图象.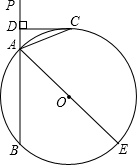 (2012•昌平区一模)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,C为⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA于D.
(2012•昌平区一模)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,C为⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA于D. 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.