题目内容
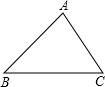如图所示，△ABC中，∠A=75°，∠B=45°，AB=4| 3 |
分析：作AE⊥BC于E，把△ABC转化成两个直角三角形，运用三角函数定义求解．
解答：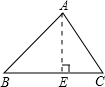
解：作AE⊥BC于E点．
在Rt△ABE中，∠B=45°，
则△ABC为等腰直角三角形，
∴AE=BE=2
；
在Rt△ACE中，
可得∠CAE=30°，
则CE=tan30°×AB=2
，
AC=
=4
，
故BC=BE+CE=2
+2
．
解：作AE⊥BC于E点．在Rt△ABE中，∠B=45°，
则△ABC为等腰直角三角形，
∴AE=BE=2
| 6 |
在Rt△ACE中，
可得∠CAE=30°，
则CE=tan30°×AB=2
| 2 |
AC=
| AE |
| cos30° |
| 2 |
故BC=BE+CE=2
| 6 |
| 2 |
点评：本题考查解斜三角形的方法：作高构造直角三角形求解．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
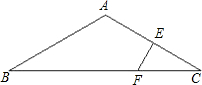如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
16、如图所示，△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、AC于D、E，∠CAE：∠EAB=5：2，则∠B=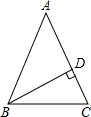
如图所示，△ABC中，AB=AC=10，BD是AC边的高线，DC=2，试求BD的长．
如图所示，△ABC中，BC的垂直平分线交AB于点E，若△ABC的周长为10，BC=4，则△ACE的周长是
如图所示，△ABC中，AB=AC，BD⊥AC，垂足为D，求∠DBC与∠A的关系．