Question

如图是某公园的一角，∠AOB=90°，弧AB的半径OA长是6米，C是OA的中点，点D在弧AB上，CD∥OB，则图中休闲区（阴影部分）的面积是________．

Answer 1

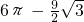
分析：先根据半径OA长是6米，C是OA的中点可知OC=OA=3米，再在Rt△OCD中，利用勾股定理求出CD的长，根据锐角三角函数的定义求出∠DOC的度数，由S_阴影=S_扇形AOD-S_△DOC即可得出结论．
解答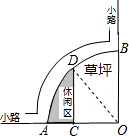：解：如图，连接OD．
∵弧AB的半径OA长是6米，C是OA的中点，
∴OC=OA=×6=3米，
∵∠AOB=90°，CD∥OB，
∴CD⊥OA，
在Rt△OCD中，∵OD=6，OC=3，
∴CD===3米，
∵sin∠DOC===，
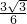∴∠DOC=60°，
∴S_阴影=S_扇形AOD-S_△DOC=-×3×3=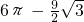（平方米）．
故答案是：．
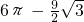点评：本题考查的是扇形的面积，根据题意求出∠DOC的度数，再由S_阴影=S_扇形AOD-S_△DOC得出结论是解答此题的关键．