题目内容
如图,AB是半圆的直径,点D是
 的中点,∠ABC=50°,则∠DAB等于( )
的中点,∠ABC=50°,则∠DAB等于( )


A.55° B.60° C.65° D.70°
C【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】计算题.
【分析】连结BD,由于点D是AC弧的中点,即弧CD=弧AD,根据圆周角定理得∠ABD=∠CBD,则∠ABD=25°,再根据直径所对的圆周角为直角得到∠ADB=90°,然后利用三角形内角和定理可计算出∠DAB的度数.
【解答】解:连结BD,如图,
∵点D是
 的中点,即弧CD=弧AD,
的中点,即弧CD=弧AD,
∴∠ABD=∠CBD,
而∠ABC=50°,
∴∠ABD=
 ×50°=25°,
×50°=25°,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣25°=65°.
故选C.


【点评】本题考查了圆周角定理及其推论:在同圆或等圆中,同弧或等弧所对的圆周角相等;直径所对的圆周角为直角.

练习册系列答案
相关题目
抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A.1 B.2 C.3 D.4



 =
=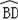
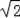
 ,求阴影部分的面积;
,求阴影部分的面积;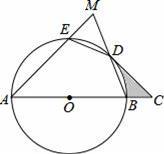


 米,则这个坡面的坡度为( )
米,则这个坡面的坡度为( )

 ,计算:
,计算:

 的值为 。
的值为 。
