题目内容
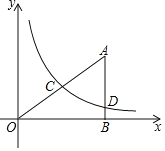
【题目】（教材呈现）下图是华师版九年级上册数学教材第78页的部分内容.
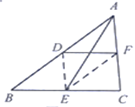
例1 求证：三角形的一条中位线与第三边上的中线互相平分.
已知：如图，在
中，
，
，
.
求证：
、
互相平分.
证明：连结
、
.
请根据教材提示，结合图①，写出完整的解题过程.
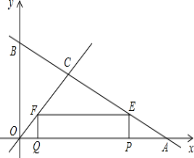
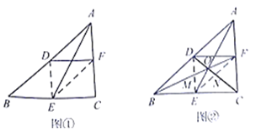
（结论应用）如图②，连结图①的
、
，分别与、、交于点
、
、
.
（1）若
，求点、之间的距离.
（2）若四边形
的面积为2，则的面积为______.
【答案】【教材呈现】答案见解析；【结论应用】（1）2；（2）24
【解析】
教材呈现：根据三角形中位线的性质可得
，从而可得四边形ADEF是平行四边形，从而可证答案；
结论应用：（1）由【教材呈现】可证点M与N分别是DE，EF的中点，从而可知MN是△DEF的中位线，从而可求答案；
（2）设MN，OE的交点为H，AE，DF的交点为P，根据【教材呈现】可知点P为DF的中点，M是DE的中点，N是DC的中点，由（1）知MN是△EDF的中位线，利用三角形中线平分面积原理即可得出答案.
教材呈现:
解：
，
，
，
同理可得
四边形
是平行四边形.
、
互相平分.
结论应用：
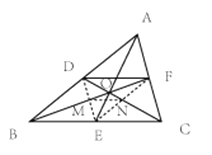
解：（1）连结
、
，如图.
，，
是
的中位线
是中线，
是
中点.
同理可得是
中点.
是
的中位线.
（2）24
理由：设MN，OE的交点为H，AE，DF的交点为P，根据【教材呈现】可知点P为DF的中点，M是DE的中点，N是DC的中点，由（1）知MN是△EDF的中位线，
∴点H是MN的中点，
∴EH是△EMN的中线，OH是△OMN的中线，
根据三角形中线平分面积可知
，
又∵四边形EMON的面积为2
∴
∵点M是DE的中点，
∴
∴
∵点N是DC的中点，
∴
∵点E是BC的中点，
∴
∵点D是AB的中点，
∴
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
