Question

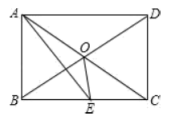
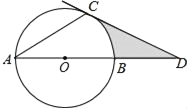
【题目】如图，AB是⊙O的直径，AC是⊙O的弦，过点C的切线交AB的延长线于点D，且∠A=∠D．

（1）求∠ACD的度数；

（2）若CD=3，求图中阴影部分的面积．

Answer 1

【答案】(1) ∠ACD=120°;(2)

【解析】

（1）连接OC，由过点C的切线交AB的延长线于点D，推出OC⊥CD，推出∠OCD=90°，即∠D+∠COD=90°，由AO=CO，推出∠A=∠ACO，推出∠COD=2∠A，可得3∠D=90°，推出∠D=30°，即可解决问题

（2）先求△OCD和扇形OCB的面积，进而可求出图中阴影部分的面积．

解：（1）连接OC，

∵过点C的切线交AB的延长线于点D，

∴OC⊥CD，

∴∠OCD=90°，

即∠D+∠COD=90°，

∵AO=CO，

∴∠A=∠ACO，

∴∠COD=2∠A，

∵∠A=∠D，

∴∠COD=2∠D，

∴3∠D=90°，

∴∠D=30°，

∴∠ACD=180°﹣∠A﹣∠D=180°﹣30°﹣30°=120°．

（2）由（1）可知∠COD=60°

在Rt△COD中，∵CD=3，

∴OC=3×

= ，

∴阴影部分的面积=