题目内容
化简:(1)
| 1 |
| x-3 |
| 1-x |
| 6+2x |
| 6 |
| x2-9 |
(2)(x2-xy)÷
| x2-2xy+y2 |
| y |
| x2-y2 |
| x2y |
分析:(1)题目是异分母分式减法,根据法则,应先通分,变为同分母的分式,再进行运算.
(2)本题分式乘除混合运算,按照从左到右的顺序进行计算,先将多项式分解因式,再约分.
(2)本题分式乘除混合运算,按照从左到右的顺序进行计算,先将多项式分解因式,再约分.
解答:解:(1)原式=
-
-
=
=
=
;
(2)原式=x(x-y)•
•
=
.
| 2(x+3) |
| 2(x-3)(x+3) |
| (1-x)(x-3) |
| 2(x+3)(x-3) |
| 12 |
| 2(x+3)(x-3) |
| x2-2x-3 |
| 2(x+3)(x-3) |
| (x-3)(x+1) |
| 2(x+3)(x-3) |
| x+1 |
| 2x+6 |
(2)原式=x(x-y)•
| y |
| (x-y)2 |
| (x+y)(x-y) |
| x2y |
| x+y |
| x |
点评:进行分式乘除法运算时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.

练习册系列答案
相关题目
(1)计算:-22+(tan60°-1)×
+(-
)-2+(-π)0-|2-
|;
(2)先化简再求值(1+
)÷
,其中x=3.
(3)物理兴趣小组20位同学在实验操作中的得分情况如下表: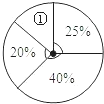
问:①求这20位同学实验操作得分的众数,中位数;
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
| 3 |
| 1 |
| 2 |
| 3 |
(2)先化简再求值(1+
| 1 |
| x-2 |
| x2-1 |
| 2x-4 |
(3)物理兴趣小组20位同学在实验操作中的得分情况如下表:

| 得分(分) | 10 | 9 | 8 | 7 |
| 人数(人) | 5 | 8 | 4 | 3 |
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?