Question

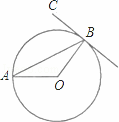
如图，AB是⊙0的弦，BC与⊙0相切于点B，连接OA、OB．若∠ABC=70°，则∠A等于（　　）

A．

15°

B．

20°

C．

30°

D．

70°

Answer 1

考点：

切线的性质。

分析：

由BC与⊙0相切于点B，根据切线的性质，即可求得∠OBC=90°，又由∠ABC=70°，即可求得∠OBA的度数，然后由OA=OB，利用等边对等角的知识，即可求得∠A的度数．

解答：

解：∵BC与⊙0相切于点B，

∴OB⊥BC，

∴∠OBC=90°，

∵∠ABC=70°，

∴∠OBA=∠OBC﹣∠ABC=90°﹣70°=20°，

∵OA=OB，

∴∠A=∠OBA=20°．

故选B．

点评：

此题考查了切线的性质与等腰三角形的性质．此题比较简单，注意数形结合思想的应用，注意圆的切线垂直于经过切点的半径定理的应用．