题目内容
由四名同学每人书写一个不同的实系数一元二次方程，他们所提供的四个方程中恰好有两个方程没有实数根的概率为
- A.
- B.
- C.
- D.
D
分析：根据已知得出假设方程为A，B，C，D，即用A无，A有表示有无实数根，列出树状图进而得出四个方程中恰好有两个方程没有实数根的概率．
解答：根据题意可以假设方程为A，B，C，D，即用A无，A有表示有无实数根，
如图所示：
∵他们所提供的四个方程中恰好有两个方程没有实数根的一共有6种，
∴他们所提供的四个方程中恰好有两个方程没有实数根的概率为：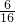
=．
故选：D．
点评：此题主要考查了树状图法求概率，树状图法适用于两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
分析：根据已知得出假设方程为A，B，C，D，即用A无，A有表示有无实数根，列出树状图进而得出四个方程中恰好有两个方程没有实数根的概率．
解答：根据题意可以假设方程为A，B，C，D，即用A无，A有表示有无实数根，
如图所示：
∵他们所提供的四个方程中恰好有两个方程没有实数根的一共有6种，
∴他们所提供的四个方程中恰好有两个方程没有实数根的概率为：
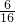=．故选：D．
点评：此题主要考查了树状图法求概率，树状图法适用于两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
，把（2）代入（1），得到正确的方程是
≤
+1的非负整数解．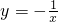
图象大致是
如图，⊙O的半径为2cm，过点O向直线l引垂线，垂足为A，OA的长为3cm，将直线l沿OA方向移动，使直线l与⊙O相切，那么平移的距离为
的解集应为