题目内容
如图,直线AB过点A(m,0)、B(0,n)(其中m>0,n>0).反比例函数y=| p | x |
 象与直线AB交于C、D两点,连接OC、OD.
象与直线AB交于C、D两点,连接OC、OD.(1)已知m+n=10,△AOB的面积为S,问:当n何值时,S取最大值?并求这个最大值;
(2)若m=8,n=6,当△AOC、△COD、△DOB的面积都相等时,求p的值.
分析:(1)根据题意,得:OA=m,OB=n,又由m+n=10,得m=10-n,进而可得S关于m、n的关系式,结合二次函数的性质计算可得答案;
(2)设直线AB的解析式为y=kx+b,根据题意,可得关于k、b的关系式,过点D、C分别作x轴的垂线,垂足分别点E、F,由△AOC、△COD、△DOB的面积都相等,可得关系式,解可得答案.
(2)设直线AB的解析式为y=kx+b,根据题意,可得关于k、b的关系式,过点D、C分别作x轴的垂线,垂足分别点E、F,由△AOC、△COD、△DOB的面积都相等,可得关系式,解可得答案.
解答:解:(1)根据题意,得:OA=m,OB=n,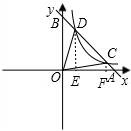
所以S=
mn,(1分)
又由m+n=10,得m=10-n,
得:S=
n(10-n)=-
n2+5n(2分)
=-
(n-5)2+
(3分)
∵-
<0,∴当n=5时,S取最大值
(4分)
(2)设直线AB的解析式为y=kx+b,
因为直线AB过点A(8,0),B(0,6)
所以
,
解得:k=-
,b=6,
所以直线AB的函数关系式为y=-
x+6(6分)
过点D、C分别作x轴的垂线,垂足分别点E、F,
当△AOC、△COD、△DOB的面积都相等时,
有S△AOC=
S△AOB,即
OA×CF=
×
OA×OB,
所以CF=2(8分)
即C点的纵坐标为2
将y=2代入y=-
x+6,得x=
(9分)
即点C的坐标为(
,2)
因为点C在反比例函数图象上
所以p=
(10分)

所以S=
| 1 |
| 2 |
又由m+n=10,得m=10-n,
得:S=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 25 |
| 2 |
∵-
| 1 |
| 2 |
| 25 |
| 2 |
(2)设直线AB的解析式为y=kx+b,
因为直线AB过点A(8,0),B(0,6)
所以
|
解得:k=-
| 3 |
| 4 |
所以直线AB的函数关系式为y=-
| 3 |
| 4 |
过点D、C分别作x轴的垂线,垂足分别点E、F,
当△AOC、△COD、△DOB的面积都相等时,
有S△AOC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
所以CF=2(8分)
即C点的纵坐标为2
将y=2代入y=-
| 3 |
| 4 |
| 16 |
| 3 |
即点C的坐标为(
| 16 |
| 3 |
因为点C在反比例函数图象上
所以p=
| 32 |
| 3 |
点评:本题考查了反比例函数的图象的性质以及其与直线的关系,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
相关题目
 D两点,P为双曲线
D两点,P为双曲线 (2009•同安区质检)如图,直线AB过点A(m,0)、B(0,n)(其中m>0,n>0).反比例函数
(2009•同安区质检)如图,直线AB过点A(m,0)、B(0,n)(其中m>0,n>0).反比例函数 (2013•房山区二模)如图,直线AB过点A,且与y轴交于点B.
(2013•房山区二模)如图,直线AB过点A,且与y轴交于点B.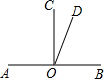 如图,直线AB过点O,OC、OD是直线AB同旁的两条射线,若∠BOD比∠COD的3倍大20°,∠AOD比∠BOD的2倍小15°,求∠COD的度数.
如图,直线AB过点O,OC、OD是直线AB同旁的两条射线,若∠BOD比∠COD的3倍大20°,∠AOD比∠BOD的2倍小15°,求∠COD的度数.