题目内容
在圆中,弦长为2且半径为2围成的弓形的面积是
- A.
 π-
π-
- B.
 π-2
π-2
- C.
 π-
π-
- D.
 π-2
π-2
A
分析:有条件可知弦长等于圆的半径,即弦所对的圆心角是60°,再根据弓形的面积等于它所在的扇形面积与所对的弦和半径构成的三角形的面积差即S弓形=S扇形-S△求解即可.
解答:∵弦长为2且半径为2,
∴弦所对的圆心角是60°,
∴S弓形=S扇形-S△= -
- ×2×
×2× =
= -
- ,
,
故选A.
点评:主要考查了弓形面积的求算方法,解题的关键是理解弓形的面积=扇形的面积-三角形的面积.
分析:有条件可知弦长等于圆的半径,即弦所对的圆心角是60°,再根据弓形的面积等于它所在的扇形面积与所对的弦和半径构成的三角形的面积差即S弓形=S扇形-S△求解即可.
解答:∵弦长为2且半径为2,
∴弦所对的圆心角是60°,
∴S弓形=S扇形-S△=
 -
- ×2×
×2× =
= -
- ,
,故选A.
点评:主要考查了弓形面积的求算方法,解题的关键是理解弓形的面积=扇形的面积-三角形的面积.

练习册系列答案
相关题目
 M与x轴没有交点,且圆心M在第一象限内,P是x轴正半轴上一动点,MQ⊥AB于Q,且MP=3cm,设OA=ycm,OP=xcm.
M与x轴没有交点,且圆心M在第一象限内,P是x轴正半轴上一动点,MQ⊥AB于Q,且MP=3cm,设OA=ycm,OP=xcm.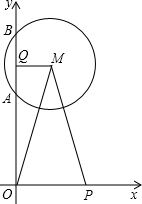 M与x轴没有交点,且圆心M在第一象限内,P是x轴正半轴上一动点,MQ⊥AB于Q,且MP=3cm,设OA=ycm,OP=xcm.
M与x轴没有交点,且圆心M在第一象限内,P是x轴正半轴上一动点,MQ⊥AB于Q,且MP=3cm,设OA=ycm,OP=xcm.
