Question

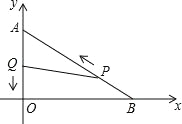
【题目】如图，在平面直角坐标系中，已知OA＝6厘米，OB＝8厘米．点P从点B开始沿BA边向终点A以1厘米/秒的速度移动；点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发运动时间为t(s).

（1）t为何值时，△APQ与△AOB相似？

（2）当 t为何值时，△APQ的面积为8cm2？

Answer 1

【答案】（1）t＝秒；（2）t＝5﹣（s）．

【解析】

（1）利用勾股定理列式求出 AB，再表示出 AP、AQ，然后分∠APQ 和∠AQP 是直角两种情况，利用相似三角形对应边成比例列式求解即可；

（2）过点 P 作 PC⊥OA 于 C，利用∠OAB 的正弦求出 PC，然后根据三角形的面积公式列出方程求解即可．

解：（1）∵点 A（0，6），B（8，0），

∴AO＝6，BO＝8，

∴AB＝ ＝＝10，

∵点P的速度是每秒1个单位，点 Q 的速度是每秒1个单位，

∴AQ＝t，AP＝10﹣t，

①∠APQ是直角时，△APQ∽△AOB，

∴，

即，

解得 t＝＞6，舍去；

②∠AQP 是直角时，△AQP∽△AOB，

∴，

即，

解得 t＝，

综上所述，t＝秒时，△APQ 与△AOB相似；

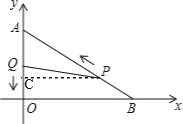
（2）如图，过点 P 作 PC⊥OA 于点C，

则 PC＝APsin∠OAB＝（10﹣t）×＝（10﹣t），

∴△APQ的面积＝×t×（10﹣t）＝8，

整理，得：t2﹣10t+20＝0，

解得：t＝5+＞6（舍去），或 t＝5﹣，

故当 t＝5﹣（s）时，△APQ的面积为 8cm2．