题目内容
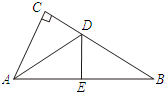如图，△ABC中，∠C=90°，AC=6，BC=8，将点C折叠到AB边的点E处，折痕为AD，则CD的长为
- A.3
- B.5
- C.4
- D.
A
分析：首先根据勾股定理计算出AB的长，再根据折叠可得AC=AE=6，CD=DE，BE=10-6=4，然后设CD=DE=x，则BD=8-x，再在直角△BDE中利用勾股定理即可算出x的值．
解答：在直角△ABC中：AB=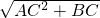
=
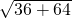=10，
根据折叠可得AC=AE=6，CD=DE，BE=10-6=4，
设CD=DE=x，则BD=8-x，
在直角△BDE中：（8-x）2=x2+42，
解得：x=3．
故选A．
点评：此题主要考查了图形的翻折变换，解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．我们运用方程解决时，应认真审题，设出正确的未知数．
分析：首先根据勾股定理计算出AB的长，再根据折叠可得AC=AE=6，CD=DE，BE=10-6=4，然后设CD=DE=x，则BD=8-x，再在直角△BDE中利用勾股定理即可算出x的值．
解答：在直角△ABC中：AB=
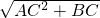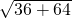==10，根据折叠可得AC=AE=6，CD=DE，BE=10-6=4，
设CD=DE=x，则BD=8-x，
在直角△BDE中：（8-x）2=x2+42，
解得：x=3．
故选A．
点评：此题主要考查了图形的翻折变换，解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．我们运用方程解决时，应认真审题，设出正确的未知数．
练习册系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．