题目内容
已知x=347，y=756，z=-100，求式子（x+y+z）（x-y-z）-（x+y-z）（x-y+z）的值．
考点：整式的混合运算—化简求值
专题：
分析：首先利用平方差公式将原始化简，进而代入已知求出即可．
解答：解：（x+y+z）（x-y-z）-（x+y-z）（x-y+z）
=[x+（y+z）][x-（y+z）]-[x+（y-z）][x-（y-z）]
=x2-（y+z）2-x2+（y-z）2
=[（y-z）+（y+z）][（y-z）-（y+z）]
=2y×（-2z）
=-4yz，
将y=756，z=-100代入得：
原式=-4×756×（-100）=302400．
=[x+（y+z）][x-（y+z）]-[x+（y-z）][x-（y-z）]
=x2-（y+z）2-x2+（y-z）2
=[（y-z）+（y+z）][（y-z）-（y+z）]
=2y×（-2z）
=-4yz，
将y=756，z=-100代入得：
原式=-4×756×（-100）=302400．
点评：此题主要考查了整式的混合运算，正确运用平方差公式是解题关键．
练习册系列答案
相关题目
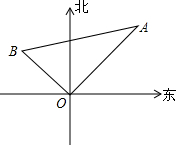如图所示，甲渔船以8海里/时的速度离开港口O向东北方向航行，乙渔船以6海里/时的速度离开港口O向西北方向航行，他们同时出发，一个半小时后，甲、乙两渔船相距多少海里？
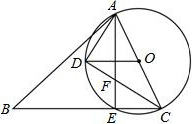如图，在锐角△ABC中，AC是最短边，以AC中点O为圆心，AC为直径作⊙O，交BC于点E，过O作OD∥BC交⊙O于点D，连结AE，AD，DC．求证：