题目内容
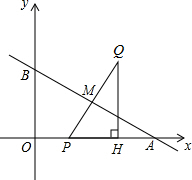 如图直线y=-
如图直线y=-| 1 | 2 |
(1)求tan∠OAB的值;
(2)当QH=2时,求P的坐标;
(3)连接OQ,是否存在t的值,使△OQH与△APM相似?若存在,求出t的值;若不存在,说明理由.
分析:(1)根据直线解析式求出点A、B的坐标,从而得到OA、OB的长度,再根据锐角的正切值等于对边比邻边列式计算即可得解;
(2)根据勾股定理求出AB的长度,再根据∠QPH的正弦等于∠OAB的余弦求出QP的长,然后根据轴对称的性质求出PM的长,再利用∠OAB的正弦值求出AP的长,再分点P在点A的左边与右边两种情况求出OP的长度,即可得到点P的坐标;
(3)分点P在点A的左边与右边两种情况,根据点P的坐标表示出AP的长,再利用∠OAB的正弦值表示出PM,根据轴对称的性质表示出PQ,利用∠QPH的正弦表示出QH,余弦表示出PH,从而可以表示出OH,再根据两边对应成比例,夹角相等,两三角形相似,分两种情况列式求解即可.
(2)根据勾股定理求出AB的长度,再根据∠QPH的正弦等于∠OAB的余弦求出QP的长,然后根据轴对称的性质求出PM的长,再利用∠OAB的正弦值求出AP的长,再分点P在点A的左边与右边两种情况求出OP的长度,即可得到点P的坐标;
(3)分点P在点A的左边与右边两种情况,根据点P的坐标表示出AP的长,再利用∠OAB的正弦值表示出PM,根据轴对称的性质表示出PQ,利用∠QPH的正弦表示出QH,余弦表示出PH,从而可以表示出OH,再根据两边对应成比例,夹角相等,两三角形相似,分两种情况列式求解即可.
解答:解:(1)令y=0,则-
x+2=0,解得x=4,
令x=0,则y=2,
所以,点A(4,0),B(0,2),
所以,OA=4,OB=2,
tan∠OAB=
=
=
;
(2)根据勾股定理,AB=
=
=2
,
∵P、Q两点关于直线AB轴对称,
∴∠OAB+∠QPH=90°,
∴sin∠QPH=cos∠OAB=
=
,
cos∠QPH=sin∠OAB=
=
,
∵QH⊥x轴,QH=2,
∴PQ=QH÷sin∠QPH=2÷
=
,
∵P、Q两点关于直线AB轴对称,PQ交AB于点M,
∴PM=
PQ=
,
∴AP=PM÷sin∠OAB=
÷
=
,
①当点P在点A的左边时,OP=OA-AP=4-
=
,
此时,点P的坐标是(
,0),
②当点P在点A的右边时,OP=OA+AP=4+
=
,
此时,点P的坐标是(
,0);
故,点P的坐标为(
,0)或(
,0);
(3)①当点P在点A的左边时,
∵点P的坐标为(t,0),
∴AP=4-t,PM=AP•sin∠OAB=
(4-t),
∵P、Q两点关于直线AB轴对称,PQ交AB于点M,
∴PQ=2PM=
(4-t),
QH=PQ•sin∠QPH=
(4-t)×
=
,
PH=PQ•cos∠QPH=
(4-t)×
=
,
当点P在点O右侧时,OH=OP+PH=t+
=
,
∵△OQH与△APM相似,
∴
=
=tan∠OAB或
=
=tan∠OAB,
即
=
或
=
,
解得t=0或t=
;
当点P在点O左侧时,OH=OP-PH=(-t)-
=-
,
∵△OQH与△APM相似,
∴
=
=tan∠OAB或
=
=tan∠OAB,
即
=
或
=
,
解得t=-16或t=8(舍去);
②当点P在点A的左边时,
∵点P的坐标为(t,0),
∴AP=t-4,PM=AP•sin∠OAB=
(t-4),
∵P、Q两点关于直线AB轴对称,PQ交AB于点M,
∴PQ=2PM=
(t-4),
QH=PQ•sin∠QPH=
(t-4)×
=
,
PH=PQ•cos∠QPH=
(t-4)×
=
,
∴OH=OP-PH=t-
=
,
∵△OQH与△APM相似,
∴
=
=tan∠OAB或
=
=tan∠OAB,
即
=
或
=
,
解得t=-16(舍去)或t=8,
综上所述,存在t的值,t=0或t=
或t=-16或t=8,使△OQH与△APM相似.
| 1 |
| 2 |
令x=0,则y=2,
所以,点A(4,0),B(0,2),
所以,OA=4,OB=2,
tan∠OAB=
| OB |
| OA |
| 2 |
| 4 |
| 1 |
| 2 |
(2)根据勾股定理,AB=
| OA2+OB2 |
| 42+22 |
| 5 |
∵P、Q两点关于直线AB轴对称,
∴∠OAB+∠QPH=90°,
∴sin∠QPH=cos∠OAB=
| 4 | ||
2
|
2
| ||
| 5 |
cos∠QPH=sin∠OAB=
| 2 | ||
2
|
| ||
| 5 |
∵QH⊥x轴,QH=2,
∴PQ=QH÷sin∠QPH=2÷
2
| ||
| 5 |
| 5 |
∵P、Q两点关于直线AB轴对称,PQ交AB于点M,
∴PM=
| 1 |
| 2 |
| ||
| 2 |
∴AP=PM÷sin∠OAB=
| ||
| 2 |
| ||
| 5 |
| 5 |
| 2 |
①当点P在点A的左边时,OP=OA-AP=4-
| 5 |
| 2 |
| 3 |
| 2 |
此时,点P的坐标是(
| 3 |
| 2 |
②当点P在点A的右边时,OP=OA+AP=4+
| 5 |
| 2 |
| 13 |
| 2 |
此时,点P的坐标是(
| 13 |
| 2 |
故,点P的坐标为(
| 3 |
| 2 |
| 13 |
| 2 |
(3)①当点P在点A的左边时,
∵点P的坐标为(t,0),
∴AP=4-t,PM=AP•sin∠OAB=
| ||
| 5 |
∵P、Q两点关于直线AB轴对称,PQ交AB于点M,
∴PQ=2PM=
2
| ||
| 5 |
QH=PQ•sin∠QPH=
2
| ||
| 5 |
2
| ||
| 5 |
| 16-4t |
| 5 |
PH=PQ•cos∠QPH=
2
| ||
| 5 |
| ||
| 5 |
| 8-2t |
| 5 |
当点P在点O右侧时,OH=OP+PH=t+
| 8-2t |
| 5 |
| 8+3t |
| 5 |
∵△OQH与△APM相似,
∴
| OH |
| QH |
| AP |
| AM |
| QH |
| OH |
| AP |
| AM |
即
| ||
|
| 1 |
| 2 |
| ||
|
| 1 |
| 2 |
解得t=0或t=
| 24 |
| 11 |
当点P在点O左侧时,OH=OP-PH=(-t)-
| 8-2t |
| 5 |
| 8+3t |
| 5 |
∵△OQH与△APM相似,
∴
| OH |
| QH |
| AP |
| AM |
| QH |
| OH |
| AP |
| AM |
即
-
| ||
|
| 1 |
| 2 |
| ||
-
|
| 1 |
| 2 |
解得t=-16或t=8(舍去);
②当点P在点A的左边时,
∵点P的坐标为(t,0),
∴AP=t-4,PM=AP•sin∠OAB=
| ||
| 5 |
∵P、Q两点关于直线AB轴对称,PQ交AB于点M,
∴PQ=2PM=
2
| ||
| 5 |
QH=PQ•sin∠QPH=
2
| ||
| 5 |
2
| ||
| 5 |
| 4t-16 |
| 5 |
PH=PQ•cos∠QPH=
2
| ||
| 5 |
| ||
| 5 |
| 2t-8 |
| 5 |
∴OH=OP-PH=t-
| 2t-8 |
| 5 |
| 3t+8 |
| 5 |
∵△OQH与△APM相似,
∴
| OH |
| QH |
| AP |
| AM |
| QH |
| OH |
| AP |
| AM |
即
| ||
|
| 1 |
| 2 |
| ||
|
| 1 |
| 2 |
解得t=-16(舍去)或t=8,
综上所述,存在t的值,t=0或t=
| 24 |
| 11 |
点评:本题是对一次函数的综合考查,主要涉及一次函数与坐标轴的交点,锐角三角形函数,相似三角形对应边成比例,解直角三角形,(2)要分点P在点A的左右两边两种情况讨论,(3)根据点P的位置的不同,分别列出OH的不同表示是解题的关键,还要根据相似三角形对应边不明确需要分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图直线y=
如图直线y=

