题目内容
4. 在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.当α=90°时,求AE′,BF′的长.
在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.当α=90°时,求AE′,BF′的长.
分析 根据点A和点B的坐标得到OA=2,OE=1,OB=2,OF=1,再根据旋转的性质得E′(0,1),F′(1,0),然后利用勾股定理计算AE′,BF′的长.
解答 解:∵点A(-2,0),点B(0,2),点E,点F分别为OA,OB的中点,
∴OA=2,OE=1,OB=2,OF=1,
∵正方形OEDF绕点O顺时针旋转90°,得正方形OE′D′F′,
∴E′(0,1),F′(1,0),
在Rt△OAE′中,AE′=$\sqrt{O{A}^{2}+OE{′}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$;
在Rt△OBF′中,BF′=$\sqrt{O{B}^{2}+OF{′}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
即AE′,BF′的长都为$\sqrt{5}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了坐标与图形性质.

练习册系列答案
相关题目
16.下列各数中是无理数的是( )
| A. | 8 | B. | $\root{3}{27}$ | C. | $\frac{13}{5}$ | D. | $\sqrt{5}$ |
13.某班开展跳绳比赛,5名同学的成绩如下(单位:个):137,140,142,138,140,这组数据的中位数是( )
| A. | 137 | B. | 138 | C. | 140 | D. | 142 |
 下面是由五块积木搭成的一个几何体,这五块积木都是棱长为1的正方体.
下面是由五块积木搭成的一个几何体,这五块积木都是棱长为1的正方体. 分别画出图中几何体的主视图,左视图和俯视图.
分别画出图中几何体的主视图,左视图和俯视图. 如图,以已知线段AB为弦作⊙O,使其经过已知点C.利用直尺和圆规作图(保留作图痕迹,不必写出作法).
如图,以已知线段AB为弦作⊙O,使其经过已知点C.利用直尺和圆规作图(保留作图痕迹,不必写出作法).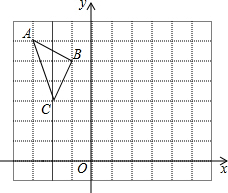 如图,已知△ABC请画出△ABC关于y轴对称的图形△A′B′C′并按要求填空.(方格的边长为1)
如图,已知△ABC请画出△ABC关于y轴对称的图形△A′B′C′并按要求填空.(方格的边长为1)